PGCD : D`Euclide à Bézout

Chapitre III
PGCD : D’Euclide à Bézout
1 PGCD de deux entiers
☞Activités 1 et 2 page 34 pour se rafraîchir la mémoire et découvrir quelques propriétés
du PGCD.
Considérons un entier relatif a. On notera D(a)l’ensemble de ses diviseurs dans Z.
Par exemple, D(0) = Z,D(1) = {−1; 1},D(12) = {−12; −6; −4; −3; −2; −1; 1; 2; 3; 4; 6; 12}.
Pour tout a∈Z,1∈ D(a).D(a)est donc non vide. De plus, |a|est le plus grand élément de
D(a).D(a)est donc majoré.
Définition 1 :
Soit aet bdeux entiers non simultanément nuls. On appelle PGCD de aet bet on note
P GCD(a;b)ou a∧ble plus grand entier naturel qui divise simultanément aet b.
Le PGCD de aet best donc le plus grand élément de D(a)∩ D(b). Comme toute partie
non vide et majorée de Nadmet un plus grand élément, cette définition en est bien une car
D(a)∩ D(b)contient au moins 1.
Exemple 1 :
1. Écrire la liste des diviseurs de 30 et de −30 puis de 12 et de −12.
2. En déduire que P GCD(30; 12) = P GCD(30; −12) = P GCD(−30; 12) = P GCD(−30; −12) =
6.
Remarque 1 Pour tous a, b ∈Z, on a P GCD(a, b) = P GCD(−a, b) = P GCD(a, −b) =
P GCD(−a, −b). On travaillera donc désormais avec des entiers naturels.
Propriété 1 : Pour tous a, b ∈Nnon simultanément nuls :
•P GCD(a;b) = P GCD(b;a)
•P GCD(a;a) = a
•P GCD(a; 0) = a
•P GCD(a; 1) = 1
•b|asi et seulement si P GCD(a;b) = b
•Pour tout k∈N,P GCD(ka;kb) = k×P GCD(a;b)
Démonstration : en classe
Définition 2 On dit que deux entiers naturels sont premiers entre eux si leur PGCD est 1.
1

2 Algorithme d’Euclide
Euclide a vécu au 3ème siècle avant notre ère en Grèce. Il est considéré comme le "père
de la géométrie". Son ouvrage le plus célèbre, les Éléments, comprenant 13 tomes est un
des plus anciens traités connus présentant de manière systématique, à partir d’axiomes et
de postulats et avec des démonstrations, un large ensemble de théorèmes sur la géométrie
et l’arithmétique. Ce traité est, paraît-il, le livre qui s’est le plus vendu au monde après la
bible.
Lemme 1 (d’Euclide) Soit aet bdeux entiers naturels non nuls et rle reste dans la
division euclidienne de apar b. Alors P GCD(a;b) = P GCD(b;r)
Idée de la démonstration : De l’égalité a=bq +r, on tire que D(a;b) = D(b;r)
Algorithme 1 (d’Euclide) :
Soit aet bdeux entiers naturels non nuls. La suite des divisions euclidiennes suivantes finit
par s’arrêter :
de apar b:a=bq0+r0, avec 0≤r0< b
de bpar r0:b=r0q1+r1avec 0≤r1< r0
de r0par r1:r0=r1q2+r2avec 0≤r2< r1
.
.
.
de rn−2par rn−1:rn−2=rn−1qn+rn
de rn−1par rn:rn−1=rnqn+1 + 0
On a alors : P GCD(a;b) = rn, dernier reste non nul.
Idée de démonstration : La suite (rn)est strictement décroissante et à valeurs dans Ndonc
il existe n0∈Ntel que rn0= 0. Le reste découle du lemme précédent.
Exemple 2 Calculer P GCD(585; 481) :
585 = 481 ×1 + 104
481 = 104 ×4 + 65
104 = 65 ×1 + 39
65 = 39 ×1 + 26
39 = 26 ×1 + 13
26 = 13 ×2 + 0
Donc P GCD(585; 481) = 13.
Remarque 2 :
– Cet algorithme, vieux de plus de 2 millénaires, est assez performant. Il a
fallu attendre la fin du 18ème siècle pour qu’un mathématicien français,
Gabriel Lamé démontre, en utilisant la suite de Fibonacci et le nombre
d’or, que cet algorithme trouve le PGCD des entiers a et b en moins de
5k étapes, où k est le nombre de chiffres décimaux de b.
2

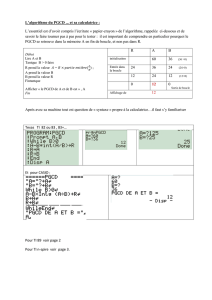
– Voici l’algorithme d’Euclide en langage Casio (bien qu’il existe une fonction donnant
directement le PGCD de deux entiers) :
"a" : ? -> a
"b" : ? -> b
While b!=0
a-b*Int(a/b)-> r
b -> a
r -> b;
WhileEnd
"PGCD(a,b)=" a
3 Théorème de Bézout
Étienne Bézout, mathématicien français né en 1730, a établi que
le PGCD de deux entiers est en fait une combinaison linéaire de
ces deux entiers. Ce résultat avait déjà été démontré au début du
17ème siècle par Bachet de Méziriac mais Bézout l’a généralisé et
a laissé son nom à la postérité.
3.1 Égalité de Bézout
Théorème 1 Soit aet bdeux entiers relatifs.
Si d=P GCD(a;b), alors il existe deux entiers uet vtels que
au +bv =d
Démonstration (du site de G.Connan) :
Considérons d’abord le cas où aet bsont non nuls et notons
S={au +bv;u∈Z, v ∈Zet au +bv > 0}
L’ensemble Sest constitué d’entiers naturels et est non vide car il contient au moins a2+b2: il
admet donc un unique plus petit élément que nous noterons dqui s’écrit donc d=au0+bv0.
Notre mission va bien sûr consister à prouver que dest en fait le PGCD de aet b.
Nous allons pour cela utiliser une ficelle classique : introduire le reste de la division eu-
clidienne de apar det utiliser le fait que dest le plus petit élément de Spuis raisonner par
l’absurde.
La division de apar ds’écrit
a=dq +ravec 0≤r < d
Supposons que r > 0, alors
r=a−dq =a−q(au0+bv0) = a(1 −qu0) + b(−qv0)>0
3

et donc r∈Sor r < d. C’est impossible car dest le plus petit élément de S:contradiction.
Notre supposition de départ est donc fausse et r= 0. Nous en déduisons que ddivise a.
On montre de manière similaire que ddivise b. Ainsi
dest un diviseur commun de aet b
Il nous reste à montrer que c’est le plus grand. Soit δun diviseur commun à aet b
quelconque. On a montré au début du cours qu’alors δdivisait toute combinaison linéaire de
aet de b, donc en particulier δdivise au0+bv0donc d. Alors toujours δ≤ |d|=d, donc dest
bien le plus grand des diviseurs.
Il faut encore vérifier que le PGCD est unique. La méthode habituelle est de supposer
qu’il existe un deuxième PGCD, disons d′. Alors d≤d′car d′est le plus grand diviseur puis
d′≤dcar daussi et finalement d=d′ce qui assure l’unicité.
Comme |a|=±1×a+ 0 ×0, l’égalité tient toujours si best nul. Il en est de même si a
est nul.
3.2 Théorème de Bézout
Théorème 2 Soit aet bdeux entiers relatifs.
aet bsont premiers entre eux si et seulement si il existe deux entiers uet vtels que
au +bv = 1.
Démonstration :
Le sens direct découle du théorème précédent.
Pour la réciproque, l’égalité au +bv = 1 entraîne que le PGCD de aet bdivise 1...
3.3 Algorithme d’Euclide étendu
Cet algorithme retourne le PGCD dde deux entiers aet bainsi que les coefficients de
Bézout uet vtels que au +bv =d.
Voir activité 46 page 49.
À partir de la suite (rn)des restes des divisions euclidiennes
de l’algorithme d’Euclide, on construit deux suites (un)et
(vn)telles que, pour tout n,rn=aun+bvn.
Initialisation : r0=a;r1=b;u0= 1 ;u1= 0 ;v0= 1 ;
v1= 1.
On a alors r0=au0+bv0et r1=au1+bv1.
Relation de récurrence : Si rn=rn+1 ×qn+1 +rn+2 est la
division de l’algorithme d’Euclide à l’étape n+ 1, on a :
rn+2 =aun+2 +bvn+2 avec un+2 =un−un+1 ×qn+1 et
vn+2 =vn−vn+1 ×qn+1. Il s’agit donc d’une relation de
récurrence d’ordre 2.
Sortie : Soit Ntel que rN+2 = 0. On a alors rN+1 =
P GCD(a;b) = auN+1 +bvN+1
En langage Casio :
4

4 Théorème de Gauss
Surnommé le Prince des mathématiciens, Carl Friedrich Gauss
(1777-1855) étudia tous les domaines des mathématiques et contri-
bua à développer la plupart des branches des sciences.
Théorème 3 Soit a, b et ctrois entiers non nuls.
Si a|bc et si bet csont premiers entre eux alors a|c.
Démonstration :
Il existe ktel que bc =ka.
D’après Bézout, il existe uet vtels que au+bv = 1 soit cau+cbv =cc’est-à-dire acu+akv =c.
Donc a|c.
Corollaire 1 Soit a, b, c trois entiers non nuls.
Si aet bdivisent cet aet bsont premiers entre eux, alors ab divise c.
5