Chapitre 6 NOMBRES FRACTIONS

Chapitre 6
ème
NOMBRES FRACTIONS
 Interpréter a
b comme quotient de l’entier a par l’entier b, c’est-à-dire comme le
nombre qui multiplié par b donne a.
 Division décimale d’un nombre entier par un entier.
 Placer le quotient de deux entiers sur une demi-droite graduée dans des cas simples.
 À l'école élémentaire, l'écriture fractionnaire est introduite en référence au partage
d'une unité.
Par exemple 7
3 est 7 fois un tiers.
Le vocabulaire relatif aux écritures fractionnaires est utilisé : « numérateur »,
« dénominateur ».
 Le programme de la classe de 6
ème
a pour objectif d’interpréter aussi 7
3 comme
- le tiers de 7
- le nombre qui multiplié par 3 donne 7 ;
- un nombre dont une valeur approchée est 2,33.

Chapitre NOMBRES FRACTIONS
1) Division décimale et quotient :
a) Technique opératoire de la division :
Exemple 1 :
On veut partager 36 € en 4 parts identiques.
Quel est le montant de chaque part ?
Effectuons la division de 36 par 4.
Le montant de chaque part est égal à 9 €.
On a
36
9
4
=
==
=
×
××
×
€.
Exemple 2 :
On veut partager 37 € en 4 parts identiques.
Quel est le montant de chaque part ?
On commence comme pour une division euclidienne.
Le reste n’étant pas égal à zéro,
on continue la division en écrivant 37=37,00.
Dès que l’on atteint la partie décimale du dividende,
on place la virgule au quotient.
On finit ici par obtenir un reste égal à zéro.
Ainsi
25
,
9
4
:
37
=
==
=
€.
Le montant de chaque part est égal à 9,25 €.
Ainsi
37
25
,
9
4
=
==
=
×
××
×
€.
Exemple 3 :
On veut partager 37 € en 9 parts identiques.
Quel est le montant de chaque part ?
Effectuons la division de 37 par 9.
On commence comme pour une division euclidienne.
Dès que l’on atteint la partie décimale du dividende,
on place la virgule au quotient.
Ainsi
11
,
4
9
:
37
≈
≈≈
≈
€.
4,11 est une valeur approchée
par défaut au centième du quotient de 37 par 9 .
Le montant de chaque part est égal à environ 4,11€.
Ainsi
37
99
,
36
11
,
4
9
≈
≈≈
≈
=
==
=
×
××
×
€.
6 3 4
9
6 3 - 0
On place la
virgule
0 0 7, 3 4
5 2 9,
6 3 - 0 1 8 - 0 2 0 2 - 0
0 0 0 7, 3 9
1 1 1 4,
6 3 - 0 1 9 - 0 1 9 - 0 1 9 - 1
5 2 9,
× 4
0 0 7, 3
1 1 4,
× 9
9 9 6, 3

Exemple 4 :
On dépense 21 € pour 25 crayons identiques.
Quel est le prix d’un crayon ?
Effectuons la division de 21 par 25.
Ainsi
84
,
0
25
:
21
=
==
=
€.
Chaque crayon coûte 0,84 €.
Remarque :
Effectuer une multiplication « n’agrandit pas toujours » le résultat.
Ici, en multipliant 25 par 0,84 , on obtient un produit 21 qui est inférieur à 25 .
On a
21
84
,
0
25
=
==
=
×
××
×
.
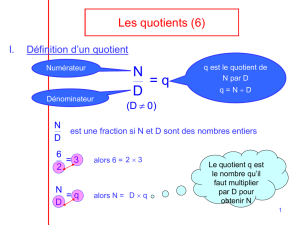
b) Définition du quotient :
Soit a un nombre entier et b un nombre entier non nul .
 On appelle « quotient de a par b » le nombre qui, multiplié par b , donne a .
 Le quotient de a par b se note a : b et correspond au résultat de la division de a par b .
On a donc
a
b
b
a
=
==
=
×
××
×
)
:
(
.
 Le quotient de a par b se note également b
a et on a l’égalité ):( ba
b
a=
==
= .
 On a également l’égalité ab
b
a=
==
=×
××
× .
c) Vocabulaire :
 On dit que b
a est « l’écriture fractionnaire » du quotient de a par b .
 On dit que a est le « numérateur » et b est le « dénominateur ».
 Quand le numérateur et le dénominateur sont des entiers, on dit que le quotient est une
« fraction ».
Exemples :
 Le quotient de 12 par 6 est 26:12
6
12 =
==
==
==
= en effet 12626
6
12 =
==
=×
××
×=
==
=×
××
×.
 Le quotient de 3 par 2 est 5,12:3
2
3=
==
==
==
= en effet 325,12
2
3=
==
=×
××
×=
==
=×
××
×.
0 0 1, 2 5 2
4 8 0,
0 - 0 1 2 0 0 2 - 0 0 1 0 0 1 - 0
5 2
×
××
× 4 8 0, 0 0 1 →25×
××
×4
0 0 0 2 →25×
××
×80
0 0 1, 2
+
++
+

Remarque :
Effectuer la division décimale de a par b , consiste à trouver le quotient dans l’égalité
a
quotient
b
=
==
=
×
××
×
donc b
a
baquotient =
==
==
==
=):( .
Exemples :
18
3
=
==
=
×
××
×
x
donc 63:18
3
18 =
==
==
==
==
==
=x et on a
18
6
3
=
==
=
×
××
×
.
176
16
=
==
=
×
××
×
y
donc 1116:176
16
176 =
==
==
==
==
==
=y et on a
176
16
11
=
==
=
×
××
×
.
13
6
=
==
=
×
××
×
z
donc 6:13
6
13 =
==
==
==
=z et on a 136
6
13 =
==
=×
××
×.
166,2
6
13 ≈
≈≈
≈
2,166 est la valeur approchée par défaut
au millième du quotient
6
13 .
On a
13
996
,
12
6
166
,
2
≈
≈≈
≈
=
==
=
×
××
×
.
d) Utilisation de la calculatrice :
...667666166,26:13
6
13 ≈
≈≈
≈=
==
=valeur donnée par la calculette.
Attention :
2,166 666 667 n’est pas la valeur exacte du quotient de 13 par 6 .
Ce n’est qu’une valeur approchée de ce quotient.
Remarque :
Le quotient
6
13
n’est pas un nombre décimal car sa partie décimale comporte un nombre infini
de chiffres.
6 7 1 6 1
1 1
6 1 - 6 1 6 1 - 0
0 0 0 3, 1 6
6 6 1 2,
2 1 - 0 1 6 - 0 4 6 3 - 0 4 6 3 - 4

2) Placer le quotient de deux entiers sur une demi-droite graduée:
Exemples :
Place sur une même demi-droite graduée les points A et B d'abscisses respectives
6
5 et
3
11 .
L’abscisse de A est égale à
6
5, on note également
6
5
A .
L’abscisse de B est égale
3
11
, on note également
3
11
B .
On choisit une longueur unité OI (par exemple
cm
OI
6
=
==
=
) que l'on partage en six parts égales.
Chacune de ces parts correspond donc à
6
1 de l'unité.
Pour placer le point A, on utilise l’égalité
6
1
5
6
5×
××
×=
==
= et on reporte donc cinq sixièmes à partir
du point O.
Pour placer le point B, on remarque que deux parts correspondent à
3
1 de l'unité et on utilise
3
1
11
3
11 ×
××
×=
==
= . On reporte donc 11 tiers à partir du point O.
Attention
3
1 correspond à deux graduations.
On peut aussi utiliser le fait que
3
2
3
3
2
3
9
3
11 +
++
+=
==
=+
++
+=
==
= et donc reporter deux tiers après 3 pour
placer le point B.
A
0
I
1
2
3
B
O
6
1
3
1
Deux parts correspondent à
3
1 de l'unité
.