TD 2 Outils pour Biologistes 2 : Cinématique

TD 2 Outils pour Biologistes 2 : Cinématique
30BU03SV – 2016-2017
Exercices encadrés
1 Cinématique et analyse de mouvement
1 2 3 4
t [s]
x [m]
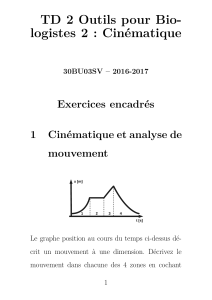
Le graphe position au cours du temps ci-dessus décrit un mouvement à une dimension.
Décrivez le mouvement dans chacune des 4 zones en cochant les cases de tous les cas qui
s’appliquent (a,b et c représentent des valeurs réelles non nulles).
Zone Mouvement
accéléré
Accélération
constante
Vitesse
constante x(t) = ct2+bt +ax(t) = bt+a x(t) = a
1
2
3
4
2 Le guépard et l’Antilope
Thème : Cinématique
Antilocapra americana (antilope d’Amérique, « pron-
ghorn ») vit dans l’ouest de l’Amérique du
Nord, dans des milieux très divers. C’est la
seule espèce d’ongulé nord-américaine endémi-
que. L’Antilope d’Amérique est l’un des ani-
maux les plus rapides de la planète pouvant
courir à 80 km/h pendant de longues périodes.
Le pronghorn a survécu à tous ses prédateurs
en courant plus vite ! Maintenant l’espèce sur-
vit encore, mais n’a guère plus de poursui-
vants. . .
Imaginons la présence d’un guépard prédateur, comme il y a des dizaines de milliers d’an-
nées quand la vitesse du pronghorn a évolué.
Un guépard est aussi un des animaux les plus rapides, mais seulement pendant de courtes
périodes de sprint caractérisées par les valeurs suivantes :
1

— vitesse maxi 120 km/h ;
— accélération de 0 à 120 km/h en 3 secondes ;
— maintien de la vitesse max (sprint) pendant environ 30 secondes.
— après le sprint à grande vitesse, ralentissement rapide à la vitesse stable de 70 km/h.
A) Pendant que le guépard accélère, quelle est son accélération moyenne ? Quelle est sa
vitesse moyenne durant cette accélération ?
B) Supposons qu’un troupeau d’antilopes pronghorns en train de courir, aperçoit devant
lui un guépard. Dès que les antilopes voient le guépard, celles-ci tournent et s’enfuient en
sens opposé de l’attaquant (pour simplification, on suppose dans cet exercice qu’elles
se retournent instantanément). À quelle distance doivent se trouver les pronghorns du
guépard quand celui-ci les surprend, pour qu’elles ne soient pas rattrapées et parviennent
à s’enfuir ? Expliquez votre raisonnement.
Exercices en autonomie
3 La chute du Faucon
Thème : cinématique, chute libre
Faucons (Falco) ainsi que « Fous de Bassan »(Morus bassanus) sont des rapaces qui se
laissent planer dans le ciel jusqu’au moment de repérer une proie. A cet instant ils re-
plient leurs ailes et se laissent pratiquement tomber en chute libre, comme une pierre,
pour fondre sur leur cible. La forme très aérodynamique vers laquelle ils ont évolué leur
permet d’atteindre une grande vitesse simplement sous l’action de la gravité, sans devoir
activement voler à vitesse élevée (cf. la figure d’un faucon en plongée ci-dessous). Dans
ce problème, on prendra l’accélération de la pesanteur g= 10 m.s−2et on néglige tout
frottement.
A. On s’intéresse ici uniquement à la cinématique en sup-
posant donc connues les équations d’un mouvement unifor-
mément accéléré (on ne demande pas d’obtenir les équations
à partir des forces). On notera z(t)l’altitude du faucon dans
un référentiel vertical orienté vers le haut avec z= 0 au ni-
veau du sol.
1. Rappelez la forme de l’équation de la vitesse en fonc-
tion du temps v(t)d’un mouvement uniformément ac-
céléré partant d’une vitesse initiale v(0).
2. Rappelez la forme de l’équation de la position en fonc-
tion du temps z(t)d’un mouvement uniformément ac-
céléré partant d’une vitesse initiale v(0) et d’une po-
sition z(0).
B. Un faucon plane lentement à une hauteur d’environ 150 mètres et voit une souris
au sol. Il replie ses ailes, commence sa plongée et accélère avec la gravité. On va calculer
dans la suite sa vitesse au moment d’arriver au niveau du sol.
On s’intéresse uniquement au mouvement vertical et on suppose qu’à l’instant initial de
chute la vitesse initiale verticale du faucon est nulle.
1. Écrivez les conditions initiales z(0) et v(0) d’après l’énoncé ci-dessus.
2. L’accélération étant la pesanteur gconstante, écrivez l’équation de variation de la
vitesse pour v(t).
2

3. Écrivez l’équation de la variation de l’altitude z(t)du faucon (sans oublier sa po-
sition initiale z(0)).
4. A partir de cette équation, à quel instant tsle faucon atteint-il le sol (z= 0 ) ?
5. Déduisez la vitesse v(ts)du faucon tout juste avant d’arriver au sol.
C. Dès que la souris aperçoit que le faucon replie ses ailes (instant de démarrage de la
chute libre) elle s’enfuit vers un refuge. À partir d’un des résultats précédents, déduisez
sans autre calcul, le temps que dispose la souris qui se trouve au sol pour s’échapper et
s’abriter.
D. Supposons que la souris coure à une vitesse de 2 m.s−1et que son comportement de
déplacement au sol ait évolué pour toujours rester à une distance d’un abris, donc rester
en dessous d’une distance maximale de sécurité. On se propose d’évaluer cette distance.
On suppose d’abord que la souris accélère instantanément à sa vitesse de course dès qu’elle
voit le faucon, c’est-à-dire à t= 0 elle a tout de suite sa vitesse de course maximale. Quelle
est la distance maximale qu’elle peut parcourir durant durant le temps de chute de celui-
ci ? Qu’elle est donc la distance de sécurité maximale ?
E. On considère maintenant une accélération. La souris est initialement au repos quand
elle aperçoit le faucon entamer sa chute. La souris accélère alors rapidement en passant
de 0 m.s−1à 2 m.s−1en 0,1 s.
1. Quelle est la valeur de son accélération ?
2. Quelle distance aura t-elle parcouru en accélérant (donc durant 0,1 s) ?
3. Tenant compte du temps, calculé plus haut, avant que n’arrive le faucon, combien
de temps reste t-il à la souris après avoir accéléré pour atteindre à temps le refuge
( durée de la fuite à la vitesse constante 2 m.s−1) ?
4. Quelle distance peut parcourir la souris durant cette phase de course à vitesse
constante ?
5. Quelle est donc la distance totale qu’elle peut parcourir en incluant la phase d’ac-
célération et la phase à vitesse constante ?
6. Concluez qu’elle est alors la distance maximale de sécurité si on tient compte de
l’accélération de la souris ? Comment se compare cette valeur avec celle calculée en
D. ? L’approximation en D. était-elle appropriée et pourquoi ?
3

Exercices d’approfondissement
4 Cinématique intégration du mouvement.
Le graphe ci-dessous indique une courbe de variation de la vitesse avec le temps.
Représentez qualitativement sur le système d’axes À droite, l’allure du mouvement sachant
que la condition initiale à t= 0 s est x(0) = 1 m.
1
t [s]
v [m/s]
1
-1
0
t [s]
x [m]
0
1
5 Mouvement d’une vésicule
Dans une étude des forces impliquées lorsque des protéines motrices déplacent des struc-
tures subcellulaires dans les cellules, Shtridleman et al. 1ont étudié le mouvement d’objets
microscopiques tel que des vésicules à l’intérieur de cellules vivantes. En utilisant des cap-
tures vidéo par microscope (voir les images données pour illustration à gauche ci-dessous),
ces auteurs ont extrait la position d’une vésicule au cours du temps. Le graphique de
droite, montre la position au cours du temps d’une des vésicules qui s’est déplacée le long
d’une ligne droite choisie pour être l’axe y.
Six positions sont identifiées sur la courbe et marqués par les lettres A à F (correspondant
à des instant t(A) à t(F)). Indiquez pour chacun des cas ci-dessous l’instant qui correspond
le mieux aux caractéristiques décrites.
1. Force-Velocity Curves of Motor Proteins Cooperating In Vivo, Y. Shtridelman, et al., Cell Biochem
Biophys. 2008, 52(1) : 19–29
4

1. L’instant où la vésicule se déplace avec la vitesse la plus élevée.
2. L’instant où la vésicule se déplace avec la vitesse la plus faible.
3. L’instant où la vésicule est soumise à l’accélération la plus grande.
4. L’instant où l’accélération est la plus importante (en valeur absolue).
Parmi les réponses possibles a) 2,0 µm.s−1; b) 0,1 µm.s−1; c) 1,0 µm.s−1, indiquez celles
qui correspondent le mieux aux questions 5 et 6.
Questions :
5. La vitesse instantanée à l’instant t(D).
6. La vitesse moyenne entre t= 0 s et t(D).
5