PLANCHE-MATH2- Manipulation des tableau Manipulation des tableaux

-1-
PLANCHE
PLANCHEPLANCHE
PLANCHE-
--
-MATH
MATHMATH
MATH2
22
2-
--
- Manipulation des tableau
Manipulation des tableauManipulation des tableau
Manipulation des tableaux
xx
x
de proportionnalité
de proportionnalitéde proportionnalité
de proportionnalité
Cette planche a une importance
Cette planche a une importance Cette planche a une importance
Cette planche a une importance hautement capitale
hautement capitalehautement capitale
hautement capitale.
..
. Il s
Il sIl s
Il s’
’’
’agit ici de savoir
agit ici de savoir agit ici de savoir
agit ici de savoir
utiliser des tableaux de proportionnalité (dit usuellement
utiliser des tableaux de proportionnalité (dit usuellement utiliser des tableaux de proportionnalité (dit usuellement
utiliser des tableaux de proportionnalité (dit usuellement tableaux en
tableaux en tableaux en
tableaux en
croix
croixcroix
croix).
).).
).
I
II
I.
. .
. Présentation
PrésentationPrésentation
Présentation d’un tableau de
d’un tableau de d’un tableau de
d’un tableau de
proportionnalité
proportionnalitéproportionnalité
proportionnalité
Un tableau de proportionnalité fait apparaître deux grandeurs de façon
proportionnelle (cette notion sera précisée ultérieurement : nous la
masquons pour le moment). Il se présente de la façon suivante :
GRANDEUR 1 Valeur 1 Valeur 2
GRANDEUR 2 Valeur 3 Valeur 4
REMARQUE IMPORTANTE
Ce tableau fait apparaître deux diagonales
deux diagonalesdeux diagonales
deux diagonales : une diagonale formée par les
nombres Valeur1 et Valeur4 ; et une autre diagonale formée par les
nombres Valeur 2 et Valeur 3.
II
IIII
II.
. .
. La règle de produit en croix
La règle de produit en croixLa règle de produit en croix
La règle de produit en croix
PRINCIPE
PRINCIPEPRINCIPE
PRINCIPE :
::
: Dans un t
Dans un tDans un t
Dans un tableau de proportionnalité comme le précédent,
ableau de proportionnalité comme le précédent, ableau de proportionnalité comme le précédent,
ableau de proportionnalité comme le précédent,
si on connait trois des valeurs, on peut facilement calculer la quatrième
si on connait trois des valeurs, on peut facilement calculer la quatrième si on connait trois des valeurs, on peut facilement calculer la quatrième
si on connait trois des valeurs, on peut facilement calculer la quatrième
valeur.
valeur.valeur.
valeur. On utilise alors la règle suivante vieille comme le monde et connue
On utilise alors la règle suivante vieille comme le monde et connue On utilise alors la règle suivante vieille comme le monde et connue
On utilise alors la règle suivante vieille comme le monde et connue
comme le pain.
comme le pain.comme le pain.
comme le pain.
REGLE TRES IMPORTANTE (DU PRODUIT EN CROIX)
REGLE TRES IMPORTANTE (DU PRODUIT EN CROIX)REGLE TRES IMPORTANTE (DU PRODUIT EN CROIX)
REGLE TRES IMPORTANTE (DU PRODUIT EN CROIX) :
::
:
Pour calculer une valeur,
Pour calculer une valeur, Pour calculer une valeur,
Pour calculer une valeur, on multiplie les
on multiplie les on multiplie les
on multiplie les deux
deux deux
deux nombres connus sur une
nombres connus sur une nombres connus sur une
nombres connus sur une
diagonale
diagonalediagonale
diagonale et
et et
et on divise par le troisième nombre connu
on divise par le troisième nombre connuon divise par le troisième nombre connu
on divise par le troisième nombre connu.
..
.
UN
UNUN
UN EXEMPLE ILLUSTRATIF
EXEMPLE ILLUSTRATIFEXEMPLE ILLUSTRATIF
EXEMPLE ILLUSTRATIF ET EXECUTION DES T
ET EXECUTION DES TET EXECUTION DES T
ET EXECUTION DES TÂCHES
ÂCHESÂCHES
ÂCHES
Calculer le nombre x dans le tableau de proportionnalité ci-dessous.
120
x
72 30

-2-
On applique à la lettre ce que dit la règle : les nombre connus
connusconnus
connus sur une
diagonale sont 120 et 30. Le troisième nombre connu est donc 72. On a
alors facilement et sans résistance :
50
72
30120 =
×
=x
EXERCICE DE COMPREHENSION
EXERCICE DE COMPREHENSIONEXERCICE DE COMPREHENSION
EXERCICE DE COMPREHENSION
Calculer les nombre
Calculer les nombre Calculer les nombre
Calculer les nombre a , b, c et d dans chacun des tableaux de
dans chacun des tableaux de dans chacun des tableaux de
dans chacun des tableaux de
proportionnalité ci
proportionnalité ciproportionnalité ci
proportionnalité ci-
--
-dessous.
dessous.dessous.
dessous.
3,6
3,63,6
3,6 a
0,18
0,180,18
0,18 4
44
4
1,6
1,61,6
1,6 0,4
0,40,4
0,4
128
128128
128 b
6
66
6 8
88
8
c 20
2020
20
d 320
320320
320
140
140140
140 200
200200
200
RAPPEL
RAPPELRAPPEL
RAPPEL TRES FONDAMENTAL
TRES FONDAMENTALTRES FONDAMENTAL
TRES FONDAMENTAL :
::
:
On multiplie
On multiplie On multiplie
On multiplie les deux nombres connus sur une diagonale
les deux nombres connus sur une diagonaleles deux nombres connus sur une diagonale
les deux nombres connus sur une diagonale (on les voit d’un
(on les voit d’un (on les voit d’un
(on les voit d’un
simple coup d’œil) et on divise par
simple coup d’œil) et on divise par simple coup d’œil) et on divise par
simple coup d’œil) et on divise par le troisième nombre connu
le troisième nombre connule troisième nombre connu
le troisième nombre connu.
..
.
 On a immédiatement 80
18,0
46,3 =
×
=a (les deux nombres connus sur une
diagonale se multiplient pendant que le troisième nombre divise).
 On a sans résistance 32
6,1
4,0128 =
×
=b .
 On obtient sans difficulté 15
8
206 =
×
=c .
 Le produit en croix fournit 224
200
320140 =
×
=d .

-3-
EXERCICE DE PREPARATION
EXERCICE DE PREPARATIONEXERCICE DE PREPARATION
EXERCICE DE PREPARATION
Un ressort s’allonge de
Un ressort s’allonge de Un ressort s’allonge de
Un ressort s’allonge de 5 cm
5 cm 5 cm
5 cm lorsqu’il supporte une masse de
lorsqu’il supporte une masse de lorsqu’il supporte une masse de
lorsqu’il supporte une masse de 800 g
800 g800 g
800 g . De
. De . De
. De
combien s’allongera
combien s’allongeracombien s’allongera
combien s’allongera-
--
-t
tt
t-
--
-il pour une masse de
il pour une masse de il pour une masse de
il pour une masse de 1280 g
1280 g1280 g
1280 g ?
??
?
NOTE
NOTENOTE
NOTE : L’allongement du ressort est proportionnel à la masse qu’il
: L’allongement du ressort est proportionnel à la masse qu’il : L’allongement du ressort est proportionnel à la masse qu’il
: L’allongement du ressort est proportionnel à la masse qu’il
supporte.
supporte.supporte.
supporte.
On construit un tableau de proportionnalité
On construit un tableau de proportionnalitéOn construit un tableau de proportionnalité
On construit un tableau de proportionnalité :
::
:
Masse (
Masse (Masse (
Masse ( en g
en gen g
en g )
))
) 800
800800
800 1280
12801280
1280
Allongement (
Allongement (Allongement (
Allongement ( en cm
en cmen cm
en cm )
))
) 5
55
5 x
xx
x
On a donc très vite
On a donc très vite On a donc très vite
On a donc très vite 8
800
12805 =
×
=x .
..
.
Le ressort s’allongera donc de
Le ressort s’allongera donc de Le ressort s’allongera donc de
Le ressort s’allongera donc de 8 cm
8 cm8 cm
8 cm pour une masse de 1280 g
pour une masse de 1280 gpour une masse de 1280 g
pour une masse de 1280 g.
..
.
UN
UN UN
UN CONSEIL
CONSEILCONSEIL
CONSEIL PRATIQUE
PRATIQUEPRATIQUE
PRATIQUE
Il faut bien penser à indiquer
Il faut bien penser à indiquer Il faut bien penser à indiquer
Il faut bien penser à indiquer les noms des
les noms des les noms des
les noms des grandeurs ainsi que les unités
grandeurs ainsi que les unitésgrandeurs ainsi que les unités
grandeurs ainsi que les unités
dans votre tableau de proportionnalité. Cela facilite la tâche du correcteur
dans votre tableau de proportionnalité. Cela facilite la tâche du correcteur dans votre tableau de proportionnalité. Cela facilite la tâche du correcteur
dans votre tableau de proportionnalité. Cela facilite la tâche du correcteur
et vous offre plus de clarté
et vous offre plus de clarté et vous offre plus de clarté
et vous offre plus de clarté et de lucidité
et de lucidité et de lucidité
et de lucidité dans le calcul.
dans le calcul.dans le calcul.
dans le calcul.
MISE EN GARDE
MISE EN GARDEMISE EN GARDE
MISE EN GARDE
Il faut faire attention à
Il faut faire attention à Il faut faire attention à
Il faut faire attention à ne pas mélanger les grandeurs
ne pas mélanger les grandeursne pas mélanger les grandeurs
ne pas mélanger les grandeurs (d’où l’intérêt de
(d’où l’intérêt de (d’où l’intérêt de
(d’où l’intérêt de
bien les ind
bien les indbien les ind
bien les indiquer dans le tableau)
iquer dans le tableau)iquer dans le tableau)
iquer dans le tableau) ; ce qui conduirait à des résultats
; ce qui conduirait à des résultats ; ce qui conduirait à des résultats
; ce qui conduirait à des résultats
catastrophiquement faux.
catastrophiquement faux.catastrophiquement faux.
catastrophiquement faux.
EXPLICATION
EXPLICATIONEXPLICATION
EXPLICATION :
::
: Dans le tableau précédent, la ligne marquée Masse (en
Dans le tableau précédent, la ligne marquée Masse (en Dans le tableau précédent, la ligne marquée Masse (en
Dans le tableau précédent, la ligne marquée Masse (en
g) ne doit contenir que des masses en g
g) ne doit contenir que des masses en gg) ne doit contenir que des masses en g
g) ne doit contenir que des masses en g ; et la ligne marquée Allongement
; et la ligne marquée Allongement ; et la ligne marquée Allongement
; et la ligne marquée Allongement
(en cm) ne doit contenir que d
(en cm) ne doit contenir que d(en cm) ne doit contenir que d
(en cm) ne doit contenir que des allongements en cm. Toute inversion
es allongements en cm. Toute inversion es allongements en cm. Toute inversion
es allongements en cm. Toute inversion
constitue une faute fatale
constitue une faute fataleconstitue une faute fatale
constitue une faute fatale de première classe
de première classede première classe
de première classe.
..
.
EXERCICE DE
EXERCICE DE EXERCICE DE
EXERCICE DE TRES HAUTE
TRES HAUTE TRES HAUTE
TRES HAUTE PREPARATION
PREPARATIONPREPARATION
PREPARATION
(
((
(EXTR
EXTREXTR
EXTREMEMENT U
EMEMENT UEMEMENT U
EMEMENT UTILE POUR LA PHYSIQUE)
TILE POUR LA PHYSIQUE)TILE POUR LA PHYSIQUE)
TILE POUR LA PHYSIQUE)
Un poids de 60 N est représenté par un vecteur de longueur 2,5 cm. Par
Un poids de 60 N est représenté par un vecteur de longueur 2,5 cm. Par Un poids de 60 N est représenté par un vecteur de longueur 2,5 cm. Par
Un poids de 60 N est représenté par un vecteur de longueur 2,5 cm. Par
quelle longueur sera représenté un poids de 48 N
quelle longueur sera représenté un poids de 48 Nquelle longueur sera représenté un poids de 48 N
quelle longueur sera représenté un poids de 48 N ?
??
?

-4-
On
On On
On forme
formeforme
forme un tableau de proportionnalité
un tableau de proportionnalitéun tableau de proportionnalité
un tableau de proportionnalité :
::
:
Poids (
Poids (Poids (
Poids ( en
en en
en N
NN
N)
))
) 60
6060
60 48
4848
48
Longueur (
Longueur (Longueur (
Longueur ( en cm
en cmen cm
en cm )
))
) 2,5
2,52,5
2,5 x
xx
x
Le produit en croix fournit alors
Le produit en croix fournit alors Le produit en croix fournit alors
Le produit en croix fournit alors 2
60
485,2 =
×
=x .
..
.
Le poids de 48 N sera donc représenté par un vecteur de longueur
Le poids de 48 N sera donc représenté par un vecteur de longueur Le poids de 48 N sera donc représenté par un vecteur de longueur
Le poids de 48 N sera donc représenté par un vecteur de longueur 2
22
2 cm
cmcm
cm.
..
.
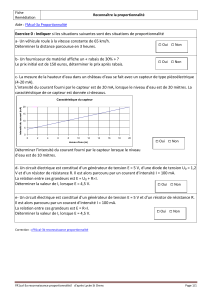
EXERCICES A FAIRE ET A RENVOYER
EXERCICES A FAIRE ET A RENVOYEREXERCICES A FAIRE ET A RENVOYER
EXERCICES A FAIRE ET A RENVOYER :
::
:
EXERCICE N°1
EXERCICE N°1EXERCICE N°1
EXERCICE N°1 :
::
:
Calculez le nombre y dans le tableau de proportionnalité ci
Calculez le nombre y dans le tableau de proportionnalité ciCalculez le nombre y dans le tableau de proportionnalité ci
Calculez le nombre y dans le tableau de proportionnalité ci-
--
-dessous
dessousdessous
dessous :
::
:
25,2
25,225,2
25,2 y
yy
y
63
6363
63 120
120120
120
EXERCICE N°
EXERCICE N°EXERCICE N°
EXERCICE N°2
22
2 :
::
:
Complétez le tableau de proportionnalité suivant en indiquant les calculs
effectué ci-dessous.
Tension électrique
(
U
)
2
3
0
…………………
420
Intensité
(
I
)
11
,5
12
…………………
EXERCICE N°
EXERCICE N°EXERCICE N°
EXERCICE N°3
33
3 :
::
:
Complétez le tableau de proportionnalité suivant en indiquant les calculs
effectué ci-dessous.
Temps (en s)
4,8
24
…………
72
Distance parcourue (en m)
…………
8
4
210
…………
EXERCICE N°
EXERCICE N°EXERCICE N°
EXERCICE N°4
44
4 :
::
:
Une force d’intensité 62 N est représentée par un vecteur de longueur
3,1 cm. Quelle sera la longueur du vecteur qui représentera une force
d’intensité 210 N.
NOTE : On présentera un tableau de proportionnalité.