Correction devoir 10

Correction DM n°10 : Recherche d’un modèle de force de frottement
Rendu le 21/12/07
A. Exploitation de l’enregistrement
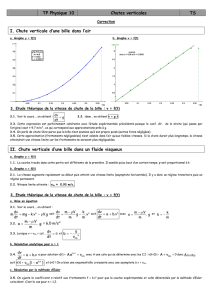
A-1. D’après le document 1, la trajectoire de la bille est une droite. D’après le document 2, la vitesse entre
M
15
et M
21
est constante. Le mouvement de la bille est donc un mouvement rectiligne uniforme.
Ceci illustre la première loi de Newton ou principe d'inertie (vecteur vitesse constant implique que la
somme des forces extérieures est nulle)
A-2. Le caméscope prend des images au rythme de 50 images par seconde, soit une durée entre deux
images de 1/50
ème
s = 0,020 s = 20 ms.
B. Étude cinématique
B-1. v
6
=
57
57
tt yy −
−
v
6
=
3-
-3
10100)-(140 1041,0)-(69,0 ×
×=
0,70 m.s
-1
B-2. Les vecteurs vitesses ont tous la même direction et le même sens (mouvement rectiligne), on peut
utiliser directement les normes : a
18 =
1719
7191
tt vv −
−
a
18
= 3
10)340380( 95,095,0 − ×−
−
= 0 m.s
-2
D’après la deuxième loi de Newton on a amF
r
r
=Σ , donc la somme des forces extérieures appliquées à la
bille est nulle ce qui entraîne (première loi de Newton) que le mouvement est rectiligne et uniforme.
Le résultat obtenu est compatible avec la question A-1.
C. Étude dynamique
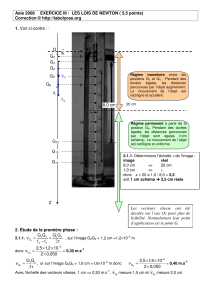
C-1. Dans un référentiel terrestre, supposé galiléen, la bille est soumise à son poids
P
r
,
à la poussée d’Archimède
A
P
r
et aux forces de frottements f
r
C-2. m = ρ
ρρ
ρ
A
×
××
×V
convertir V en m
3
m = 0,52 × 10
–6
×7850 = 4,1×10
-3
kg = 4,1 g
C-3. P
A
= m
H
×g = ρ
ρρ
ρ
H
×
××
×V×g
P
A
= 920 × 0,52 × 10
–6
×9,8 = 4,7×10
–3
N
D. Équation différentielle du mouvement de la bille
D-1. Théorème du centre d’inertie (deuxième loi de Newton) : dans un référentiel galiléen, la somme
vectorielle des forces extérieures appliquées à un solide de masse m, est égale au produit de cette masse
par le vecteur accélération de son centre d’inertie.
Gext
amF
r
r
×=Σ Soit
GA
amfPP
r
r
r
r
×=++
En projetant sur l’axe vertical représenté sur le document n°1 il vient : P – P
A
– f = m×a
G
= m×
dt
dv
En divisant par m on a :
dt
dv +
m
f =
m
PP
A
−
= A car P, P
A
et m sont des constantes.
D-2. A =
m
PP
A
−
=
m
Pgm
A
−×
= VgVgV
A
HA
×
×
×
−
×
×
ρ
ρ
ρ
= g ×
−
A
HA
ρρρ
A = 9,8
×
−
7850
9207850 =
8,7 m.s
-2
Pour t = 0 s, v = 0 alors f = 0 N donc
dt
dv = A La constante A est homogène à une accélération.
f
r
A
P
r
P
r

E. Recherche de modèles pour la force de frottement
E-1. Première hypothèse : f = k
1
.v
E-1.a) On a :
dt
dv +
m
f = A soit
dt
dv +
m
.vk
1
= A
On a bien
dt
dv +
.vB
1
= A avec B
1
=
m
k
1
E-1.b) Quand la vitesse limite est atteinte, cette valeur est constante, donc
dt
dv =0
B
1
.v
lim
= A donc B
1
=
lim
vA
Et B
1
=
m
k
1
soit k
1
= m.B
1
= m
lim
vA
k
1
= 95,0 7,8 101,4
3
××
−
= 3,7×10
–2
kg.s
-1
car A en m.s
–2
, v
lim
en m.s
–1
, m en kg
calcul effectué avec la valeur non arrondie de A
E-2. f = k
2
.v² et
dt
dv + B
2
. v² = A
quand v = v
lim
alors
dt
dv = 0
B
2
. v
lim
² = A
B
2
=
2
lim
vA
B
2
=
m
k
2
(même raisonnement que pour la question E-1.a)
soit
2
lim
vA =
m
k
2
k
2
=
2
lim
vA
m
k
2
=
2
3
95,0 7,8
101,4 ××
−
= 4,0×10
–2
kg.m
-1
car A en m.s
–2
, v
lim
² en m².s
–2
et m en kg
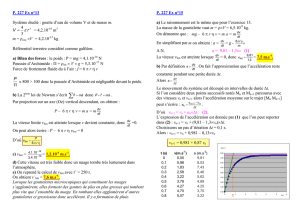
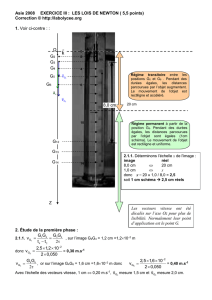
E-3. Pour 0
≤
v
≤
0,8 m.s
–1
, il semble que le modèle 1 convienne mieux.
Pour 0,8
≤
v
≤
1 m.s
–1
, il semble que ce soit le modèle 2 qui convienne.