DS de physique de décembre TS3

TS3 Correction DS de Physique décembre 2010
Exercice 1 :
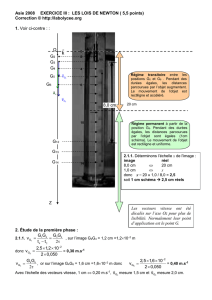
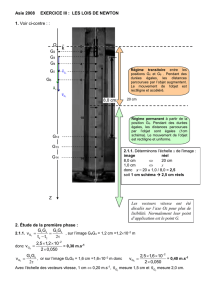
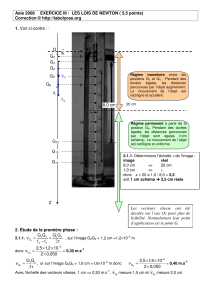
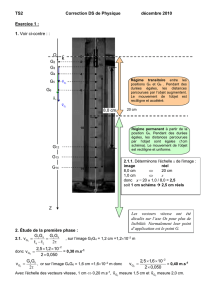
1. Voir ci-contre : :
2. Étude de la première phase :
2.1.1.
3
2 4 2 4
42 2
GG G G G
vtt
, sur l’image G2G4 = 1,2 cm =1,210–2 m
donc
3
2
G2,5 1,2 10
v2 0,050
= 0,30 m.s-1
5
46
2
GGG
v
, or sur l’image G4G6 = 1,6 cm =1,610–2 m donc
5
2
G2,5 1,6 10
v2 0,050
= 0,40 m.s-1
Avec l’échelle des vecteurs vitesse, 1 cm  0,20 m.s-1,
3
G
v
mesure 1,5 cm et
5
G
v
mesure 2,0 cm.
0
2
4
6
10
14
Z
O
20 cm
Régime transitoire entre les
positions G0 et G8 . Pendant des
durées égales, les distances
parcourues par l’objet augmentent.
Le mouvement de l’objet est
rectiligne et accéléré.
Régime permanent à partir de la
position G9. Pendant des durées
égales, les distances parcourues
par l’objet sont égales (1cm
schéma). Le mouvement de l’objet
est rectiligne et uniforme.
G2
G4
G6
G3
G5
3
G
v
5
G
v
k
4
a
G13
G12
G14
Les vecteurs vitesse ont été
décalés sur l’axe Oz pour plus de
lisibilité. Normalement leur point
d’application est le point G.
2.1.1. Déterminons l’échelle x de l’image :
image réel
8,0 cm  20 cm
1,0 cm  x
donc x = 20  1,0 / 8,0 = 2,5
soit 1 cm schéma  2,5 cm réels
8,0 cm

2.1.2.
53
53
422
GG
GGv v .k
vv
v
at . .
=
4
a .k
où
k
vecteur unitaire porté par l’axe Oz.
Ainsi :
40,40 0,30
a2 0,050
= 1,0 m.s-2.
Avec l’échelle des accélérations, 1 cm  0,50 m.s-2,
4
a
mesure 2,0 cm.
2.2. Étude théorique
2.2.1. Poussée d’Archimède : = mfluide déplacé . g = .V.g =
= 1240  2,10.10-6  9,8 = 2,6  10–2 N
Poids de la bille : P = m . g
Pm
.V
= 1,46 donc P et sont du même ordre de grandeur.
2.2.2. Le solide est soumis :
- à son poids
P
: force verticale et dirigée vers le bas
- la poussée d’Archimède : force verticale et dirigée vers le haut
- la force de frottement
f
: force verticale et dirigée vers le haut car
opposée au sens de déplacement du solide.
2.3. Deuxième loi de Newton : Dans un référentiel galiléen, la somme des forces
extérieures appliquées à un système mécanique est égale au produit de la masse
du système par le vecteur accélération de son centre d’inertie G :
ext G
F m.a
.
2.4. En appliquant la deuxième loi de Newton au solide dans le référentiel du laboratoire galiléen :
P
+ +
f
=
G
m.a
 P.
k
– .
k
– f.
k
= m.az.
k
avec f , la norme de la force de frottement
en projection sur l’axe (Oz) au point G4 :
P – – f = m.a4
f = P – – m.a4 = m.g – .V.g – m.a4
application numérique :
f = 3,8010–3  9,8 – 12402,1010–69,8 – 3,8010–31,0
f = 7,910–3 N.
2.5. L’énoncé donne : v4 = 0,32 m.s-1. (remarque : graphiquement on trouve v4 = 0,38 m.s–1, ce qui
illustre la précision de la méthode)
Or : f = k.v4 soit k =
4
f
v
k =
3 7,9 10
0,32
= 2,510–2 kg.s-1 ( car f en N avec N = kg.m.s-2 et v en m.s-1).
3. Étude de la deuxième phase
3.1. Durant la seconde phase, en régime permanent, le mouvement est rectiligne et uniforme.
3.2. Première loi de Newton : Dans un référentiel galiléen, un solide soumis à un ensemble de forces qui
se compensent est soit immobile, soit en mouvement rectiligne et uniforme. Et réciproquement.
3.3. On a :
P
+ +
f
=
0
 P – – f = 0
Posons v = vlim = Cte alors
P – – k.vlim = 0
 vlim =
P m.g .V.g g.(m .V)
k k k
 vlim =
36
2
9,8 (3,80 10 1240 2,10 10 )
2,5 10
= 0,47 m.s-1.
P
G
f
z
O
k

3.4.
13
12 14
2
GGG
v
. Or sur l’image G12G14 = 2,0 cm = 2,0.10-2 m donc
5
2
G2,5 2,0.10
v2 0,050
= 0,50 m.s-1
On trouve une valeur proche de la vitesse limite calculée.
Exercice 2 : Chute libre
1/ Système : {fléchette}
Référentiel terrestre supposé galiléen
Bilan des forces : le poids
D’après la deuxième loi de Newton :
ext G
F m.a
P
=
G
m.a
=
m.g
donc
G
ag
Caractéristiques de
G
a
:
- origine : le centre de gravité G de la fléchette
- direction : verticale
- sens : vers le bas
- a = g
2/
G
a
 - g or a = dv/dt donc
v
 -gt + C1 or à t = 0
0
v
 5 donc
v
 -gt + 5
or v = dz/dt donc
OG
 -O,5 t2 + 5t + C2 or à t=0
0
OG
 1,75 donc
OG
 -0,5 t2 + 5t +1,75
donc vZ(t) = -gt+5
et z(t) = -0,5t2 +5t +1,75
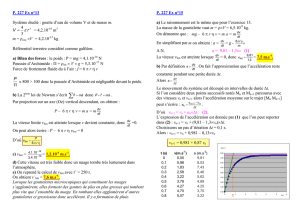
3/ a. Au sommet de la trajectoire , vZ = 0
b. Donc –gtS + 5 = 0 donc tS = 5/g = 0,51 s
c. hS = zmax = -0,5 t S 2 + 5tS +1,75 = 3,0 m
4/ La fléchette touche le sol pour z = 0
-0,5 t2 + 5t +1,75 = 0
 = 59,3
2 racines : t1 = - 0,27 s (non retenue) et t2 = 1,3 s