Asie 2008 EXERCICE III : LES LOIS... Correction © 1. 2. Étude de la première phase :

Asie 2008 EXERCICE III : LES LOIS DE NEWTON ( 5,5 points)
Correction © http://labolycee.org
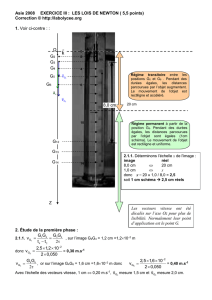
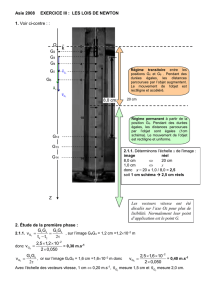
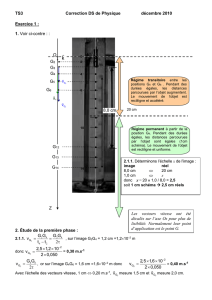
1. Voir ci-contre : :
2. Étude de la première phase :
2.1.1.
3
2 4 2 4
4 2
2
= =
− τ
G
G G G G
vt t , sur l’image G
2
G
4
= 1,2 cm =1,2×10
–2
m
donc
−
× ×
=×
3
2
G
2,5 1,2 10
v
2 0,050
= 0,30 m.s
-1
5
4 6
2
G
G G
v=
τ
, or sur l’image G
4
G
6
= 1,6 cm =1,6×10
–2
m donc
−
× ×
=×
5
2
G
2,5 1,6 10
v
2 0,050
= 0,40 m.s
-1
Avec l’échelle des vecteurs vitesse, 1 cm ⇔ 0,20 m.s
-1
,
3
G
v
mesure 1,5 cm et
5
G
v
mesure 2,0 cm.
0
2
4
6
10
14
Z
O
20 cm
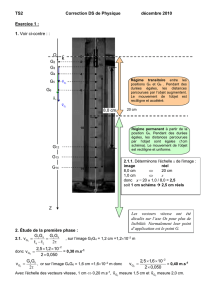
Régime transitoire
entre les
positions G
0
et G
8
. Pendant des
durées égales, les distances
parcourues par l’objet augmentent.
Le mouvement de l’objet e
st
rectiligne et accéléré.
Régime permanent
à partir de la
position G
9
. Pendant des durées
égales, les distanc
es parcourues
par l’objet sont égales (1cm
schéma). Le mouvement de l’objet
est rectiligne et uniforme.
G
2
G
4
G
6
G
3
G
5
3
G
v
5
G
v
k
4
a
G
13
G
12
G
14
Les vecteurs vitesse ont été
décalés sur l’axe Oz pour plus de
lisibilité. Normalement leur point
d’application est le point G.
2.1.1.
Déterminons l’échelle x de l’image :
image réel
8,0 cm ⇔ 20 cm
1,0 cm ⇔ x
donc x = 20 ×
××
× 1,0 / 8,0 = 2,5
soit 1 cm schéma   2,5 cm réels
8,0 cm

2.1.2.
(
)
5 3
5 3
4
2 2
G G
G G
v v .k
v v
v
a
t . .
−
−
∆
= = =
∆ τ τ
= 4
a .k
où
k
vecteur unitaire porté par l’axe Oz.
Ainsi :
−
=×
4
0,40 0,30
a
2 0,050
= 1,0 m.s
-2
.
Avec l’échelle des accélérations, 1 cm ⇔ 0,50 m.s
-2
,
4
a
mesure 2,0 cm.
2.2. Étude théorique
2.2.1. Poussée d’Archimède :
Π
= m
fluide déplacé
. g = ρ.V.g =
Π
= 1240 ×
××
× 2,10.10
-6
×
××
× 9,8 = 2,6 ×
××
× 10
–2
N
Poids de la bille : P = m . g
=
Π ρ
P m
.V
= 1,46 donc P et
Π
sont du même ordre de grandeur.
2.2.2. Le solide est soumis :
- à son poids
P
: force verticale et dirigée vers le bas
- la poussée d’Archimède
Π
: force verticale et dirigée vers le haut
- la force de frottement
f
: force verticale et dirigée vers le haut car
opposée au sens de déplacement du solide.
2.3. Deuxième loi de Newton : Dans un référentiel galiléen, la somme des forces
extérieures appliquées à un système mécanique est égale au produit de la masse
du système par le vecteur accélération de son centre d’inertie G : Σ =
ext G
F m.a
.
2.4. En appliquant la deuxième loi de Newton au solide dans le référentiel du laboratoire galiléen :
P
+
Π
+
f
=
G
m.a
⇔ P.
k
–
Π
.
k
– f .
k
= m.a
z
.
k
avec f , la norme de la force de frottement
en projection sur l’axe (Oz) au point G
4
:
P –
Π
– f = m.a
4
f = P –
Π
– m.a
4
= m.g – ρ.V.g – m.a
4
application numérique :
f = 3,80×10
–3
× 9,8 – 1240×2,10×10
–6
×9,8 – 3,80×10
–3
×1,0
f = 7,9×
××
×10
–3
N.
2.5. L’énoncé donne : v
4
= 0,32 m.s
-1
. (remarque : graphiquement on trouve v
4
= 0,38 m.s
–1
, ce qui
illustre la précision de la méthode)
Or : f = k.v
4
soit k =
4
f
v
k =
−
×
3
7,9 10
0,32
= 2,5×
××
×10
–2
kg.s
-1
( car f en N avec N = kg.m.s
-2
et v en m.s
-1
).
3. Étude de la deuxième phase
3.1. Durant la seconde phase, en régime permanent, le mouvement est rectiligne et uniforme.
3.2. Première loi de Newton : Dans un référentiel galiléen, un solide soumis à un ensemble de forces qui
se compensent est soit immobile, soit en mouvement rectiligne et uniforme. Et réciproquement.
3.3. On a :
P
+
Π
+
f
=
0
⇔ P –
Π
– f = 0
Posons v = v
lim
= Cte alors
P –
Π
– k.v
lim
= 0
⇔ v
lim
=
− Π − ρ
= = − ρ
P m.g .V.g g
.(m .V)
k k k
⇔ v
lim
= − −
−
× × − × ×
×
3 6
2
9,8
(3,80 10 1240 2,10 10 )
2,5 10
= 0,47 m.s
-1
.
3.4.
13
12 14
2
G
G G
v=
τ
. Or sur l’image G
12
G
14
= 2,0 cm = 2,0.10
-2
m donc
−
×
=×
5
2
G
2,5 2,0.10
v
2 0,050
= 0,50 m.s
-1
On trouve une valeur proche de la vitesse limite calculée.
P
Π
G
f
z
O
k