Correction des exercices sur la chute verticale

Correction des exercices sur la chute verticale
Exercice 10 p 226
a. P = m.g0 = 123,4.103 x 9,809 = 1,210 MN ;  = air.V.g0 = 1,3 x 1,132 x 9,809 = 14 kN.
b.
P '=m.g0.
RT
2
RTh²=123,4.10 ³ x9,809 x[6380.10³ ]² 6380.10³32000 x0,348²=1,206 MN
'=1
3air V.g0.
RT
2
RTh²=1,3 3x1,132 x9,809 x[6380.10³]² 6380.10³32000x0,348²=4,8 kN
Exercice 11 p 226-227
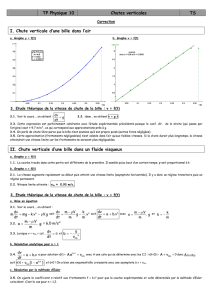
a. A partir de t = 200 ms, la valeur de la vitesse ne varie plus, le mouvement de la bille est rectiligne
uniforme, on a atteint la vitesse limite. A partir de cet instant, la force de frottement et la poussée
d'Archimède compensent le poids de la bille. La valeur de cette vitesse est 0,25 m.s-1.
b.
Exercice 13 p 227
a. Une gouttelette est soumise à son poids, à une force de frottement qui augmente avec la vitesse, et à la
poussée d'Archimède. La masse volumique de l'air étant beaucoup plus faible que celle de l'eau, on peut
négliger la poussée d'Archimède.
b. Lorque la vitesse limite est atteinte, les valeurs des deux forces sont égales. On a donc :
6...r.vlim=m.g⇒vlim=m.g
6...r=
4
3.r³.eau .g
6...r=2.r².eau .g 9.
c.
vlim=2x1.10−6²x1000 x9,81
9x18.10−6=1,2 .10−4m.s−1
d. Cette valeur de 0,12 mm par seconde est très faible, l'expression est donc justifiée.
e.
vlim=2.250.r².eau .g
9.=2x250 x1.10−6²x1000 x9,81
9x18.10−6=7,5 m.s−1
. Il s'agit cette fois d'une vitesse
importante !
Exercice 18 p 228
1. La seule force qui agit sur la bille est son poids. On peut donc écrire :
m.  g=m. aG
. Si l'on projette cette
relation sur un axe vertical dirigé vers le haut, on obtient aG = - g.
Tout le mouvement s'effectue suivant l'axe vertical, on va donc intégrer cette relation, par rapport au temps,
uniquement selon z.
aG=dvz
dt =−g⇒vz=−g.tcste
. A t = 0, vz = v0, donc cste = v0. Donc la première équation horaire est :
vz=−g.tv0
.
Nous allons intégrer une deuxième fois cette équation par rapport au temps :
vz=dz
dt =−g.tv0⇒z=−1 2.g.t²v0.tcste
. A t = 0, z = z0, donc cste = z0. La deuxième équation horaire
1/2 Document OpenOffice.org sous Debian 4.0 le 28 avr. 2008
0 50 100 150 200 250 300 350
0
0,025
0,05
0,075
0,1
0,125
0,15
0,175
0,2
0,225
0,25
t (ms)
v (m/s)
L'intersection de la tangente à l'origine
avec l'asymptote de la courbe permet de
trouver la valeur du temps caractéristique,
qui vaut ici 60 ms.

est donc :
z=−1
2.g.t²v0.tz0
2.a. Le point le plus est celui pour lequel la vitesse est nulle. La première équation nous donne :
vz=0=−g.tv0⇒t=v0
g=
36
3,6
9,8 =1,0 s
. Et si on remplace cette valeur dans la seconde équation on obtient :
zmax=−0,5 x9,8 x1,0²36
3,6 x1,02,0=7,1 m
.
2.b. Lorsque la bille atteint le sol, z = 0 dans la deuxième équation. Il faut donc la résoudre.
−0,5 x9,8. t²10,0.t2,0=0⇔−4,9 .t²10,0. t2,0=0
=10,0²4x4,9 x2,0=139,2 ⇒t1=−10,0−
139,2
−9,8 =2,2 set t2=−10,0
139,2
−9,8 =−0,18s
La deuxième solution, qui conduit à un temps négatif, n'a, bien évidemment, aucun sens physique !
2.c. La vitesse est donnée par la première équation : vz = - 9,8 x 2,2 + 10,0 = - 11,5 m.s-1.
Cette fois-ci, le signe "moins" exprime le fait que la vitesse est dirégiée vers le bas, tandis que l'axe est vers
le haut.
Exercice 23 p 228
Il faut d'abord calculer l'expression de la vitesse limite dans le cas où on utilise la formule de Stokes et dans
le cas où on utilise la formule du Cx.
Si on utilise la formule de Stokes, l'équation différentielle est :
m.g−f.V.g−6..r.v=m. dv
dt
. Quand on atteint la vitesse limite,
dv
dt =0
. Ce qui conduit à :
m.g−f.V.g−6..r.vlim=0⇒vlim=m−f.V.g
6..r=−f.V.g 6..r=2.−f.r².g 9.
car
V=4
3.r³
.
Si on utilise la formule du Cx, l'équation différentielle est :
m.g−f.V.g−Cx..v²
2.S=m. dv dt
. Quand on atteint la vitesse limite,
dv
dt =0
. Ce qui conduit à :
m.g−f.V.g−Cx..vlim²
2.S=0⇒Cx..vlim ² 2.S=m−f.V.g⇒vlim=
2.m−f.V.g
Cx..S
⇒vlim=
2. −f.V.g
Cx. .S=
2. −f.4
3..r³.g
Cx. ..r² =
8.−f.r.g
Cx. .3
Nous allons maintenant utiliser un tableur qui va nous simplifier la tâche pour calculer les vitesses limites et
le nombre de Reynolds dans les 4 cas.
On constate donc que la formulede Stokes peut être utilisée pour les cas 1 et 3, tandis que pour les cas 2 et 4
il faut utiliser la formule du Cx.
2/2 Document OpenOffice.org sous Debian 4.0 le 28 avr. 2008
1 2 3 4
r (m) 1,00E-06 1,00E-03 1,50E-02 1,00E-02 7800
1,3 1,3 1260 1000 g = 9,81
1,80E-05 1,80E-05 1,50E+00 1,10E-03 Cx = 0,44
0 944,51 2,14 1347,64
Re = 0 136429,11 53,89 24502479,34
0,01 0,24 0,86 0,72 si f f proport. à v²
Re = 0 35,22 21,79 13089,92
=
f (kg.m-3)
 (N.s.m-2)
vlim = si f f proport. à v
vlim =