TP Physique 10 Chutes verticales TS I. Chute verticale d`une bille

TP Physique 10 Chutes verticales TS
Correction
I. Chute verticale d’une bille dans l’air
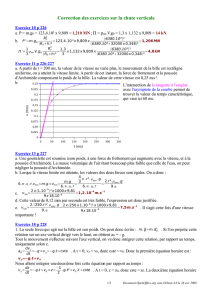
a. Graphe y = f(t) b. Graphe v = f(t)
3. Etude théorique de la vitesse de chute de la bille : v = f(t)
3.1. Voir le cours…. on obtient :
g
dt
dv
=
3.2. idem… on obtient v = g.t.
3.3. Cette expression est parfaitement cohérente avec l’étude expérimentale précédente puisque le coef. dir. de la droite (qui passe par
l’origine) vaut ≈ 9,7 m/s², ce qui correspond aux approximations prés à g.
3.4. On parle de chute libre parce que la bille n’est soumise qu’à son propre poids (autres fores négligées).
3.5. Cette approximation (frottements négligeables) n’est valable dans l’air qu’aux faibles vitesses. Si la chute durait plus longtemps, la vitesse
atteindrait une vitesse limite car les frottements ne seraient plus négligeables.
II. Chute verticale d’une bille dans un fluide visqueux
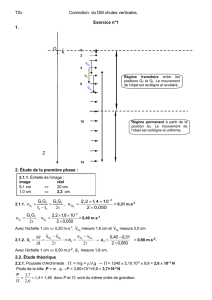
a. Graphe y = f(t)
1.1. La courbe tracée dans cette partie est différente de la première. Il semble qu’au bout d’un certain temps, y soit proportionnel à t.
b. Graphe v = f(t)
2.1. La vitesse augmente rapidement au début puis atteint une vitesse limite (asymptote horizontale). Il y a donc un régime transitoire puis un
régime permanent.
2.2. Vitesse limite atteinte : v
lim
≈ 0,93 m/s .
3. Etude théorique de la vitesse de chute de la bille : v = f(t)
a. Mise en équation
3.1. Voir le cours…. on obtient :
g.Vv.kmg
dt
dv
m
n
ρ−−=
soit
n
v.
m
k
g
m
V
m
dt
dv
−
ρ−
=
soit
n
v.ba
dt
dv
+=
avec
g.
m
V
.
m
a
ρ
−
=
et
m
k
b−=
3.2.
g.
m
V
.
m
a
ρ
−
=
= 6,0 m/s²
3.3. Lorsque v = v
lim
= cst ,
0=
dt
dv
et
n
lim
v
a
b−=
b. Résolution analytique pour n = 1
3.4.
v.ba
dt
dv
+=
a pour solution v(t) =
lim
t
.
b
v
e
.
A
+
avec A une cste qui se détermine avec les C.I : v(t=0) =
lim
v
A
+
= 0 donc A = - v
lim
soit v(t) =
)
e
(
v
t
.
b
lim
−1
et b<0 ! On a bien une exponentielle croissante avec une asymptote à v = v
lim
.
c. Résolution par la méthode d’Euler
3.5. On ajuste le coefficient n relatif aux frottements f = k.v
n
pour que la courbe expérimentale et celle déterminée par la méthode d’Euler
coïncident. C’est le cas pour n = 1,2.