TRIGONOMETRIE

TRIGONOMETRIE
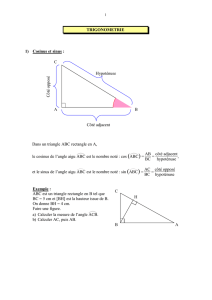
Dans toutes les formules ci-dessous, on considère un triangle ABC rectangle en A.
On note : « adj » pour côté adjacent, « hyp » pour hypoténuse et « opp » pour côté opposé.
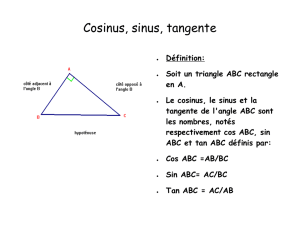
Définitions :
1) Le cosinus de l'angle
̂
ABC
est donné par
cos(
̂
ABC)= AB
BC
. (
cos=adj
hyp
)
2) Le sinus de l'angle
̂
ABC
est donné par
sin(
̂
ABC )= AC
BC
. (
sin=opp
hyp
)
3) La tangente de l'angle
̂
ABC
est donné par
tan (
̂
ABC)= AC
AB
. (
tan=opp
adj
)
Propriété : On a :
cos(
̂
ABC)2+sin (
̂
ABC )2=1
et
tan (
̂
ABC)= sin (
̂
ABC )
cos(
̂
ABC )
.
Exemples : Faites les dessins pour mieux comprendre les situations.
1) ABC est un triangle rectangle en A tel que BC=10cm et
̂
ABC=35 °
. Calculer AB en
arrondissant au millimètre.
On a :
cos(
̂
ABC)= AB
BC
. D'où
cos(35°)= AB
10
et
AB=10×cos(35°)≃8,2 cm.
2) EFG est un triangle rectangle en A tel que EG=20cm et
̂
EFG=42°
. Calculer GF en
arrondissant au dixième.
On a :
sin(
̂
EFG )= EG
EF
. D'où
sin(42 °)= 20
EF
et
EF =20
sin (42°)≃29,9cm.
3) PES est un triangle rectangle en E tel que PE=14cm et ES=9cm. Calculer l'angle
̂
EPS
.
On a :
tan (
̂
EPS )= ES
EP =9 14
. En arrondissant au degré, on obtient :
̂
EPS ≃33 °
.
Il faut taper sur la calculatrice (mais pas trop fort) sur les touches shift/seconde tan 9 : 14 ) exe
pour obtenir une approximation de l'angle
̂
EPS
. Si dans la formule, on utilise le cosinus ou le
sinus au lieu de la tangente, alors on remplace la touche tan par cos ou sin.