3 médiatrices et hauteurs - ClicProf

3
3M MÉDIATRICES ÉDIATRICES ET ET HAUTEURS HAUTEURS
5_4 espace et géométrie.odt clicprof.free.fr 10/13

1
1Définir une médiatrice et la construire à l'équerre Définir une médiatrice et la construire à l'équerre
Soyons curieux
1.1) Définition
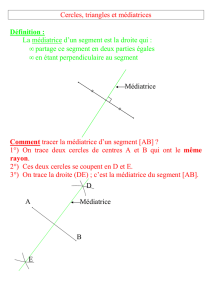
La médiatrice d'un segment est la droite qui passe par le milieu de ce segment et qui est
perpendiculaire à ce segment.
1.2) Construire la médiatrice d'un segment avec une règle graduée et
une équerre
Énoncé :
Tracer un segment et construire la médiatrice à ce segment.
Solution :
Avec une règle graduée, on mesure la
longueur du segment et on place son milieu.
Avec une équerre, on construit la droite
perpendiculaire à ce segment et passant par
son milieu.
On prolonge la droite obtenue sans oublier de
coder la figure.
5_4 espace et géométrie.odt clicprof.free.fr 11/13
Médiatrice de [AB]

2
2Caractériser une médiatrice et la construire au Caractériser une médiatrice et la construire au
compas
compas
Soyons curieux
Théorème de Johnson (1916) : Si les cercles bleus (de même rayon) on
un point commun alors il existe un cercle rouge qui passe par les trois
autres points d'intersections ayant aussi le même rayon.
« Il reste une mine de propriétés géométriques encore cachées »D Wells
Alors à vos stylos et feuilles blanches...
2.1) Définition
Lorsqu'un point M est à la même distance de deux points A et B, on dit que M est équidistant
de A et de B.
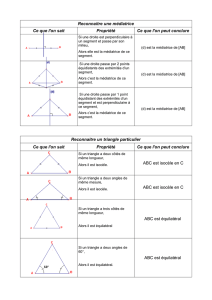
2.2) Propriétés
•Si un point appartient à la médiatrice d'un segment alors ce
point est équidistant des extrémités de ce segment.
•Si un point est équidistant des extrémités d'un segment alors
ce point appartient à la médiatrice de ce segment.
2.3) Construire la médiatrice d'un segment avec un compas
Énoncé : Tracer à l'aide du compas la médiatrice d'un segment [AB]
Solution :
1. On prend un écartement de compas (plus grand que la
moitié du segment), et on le conserve tout au long de la
construction.
2. On place la pointe sur chacune des extrémités du segment
et on trace ainsi deux arcs de cercle.
3. On trace la droite passant par les deux points
d'intersections des deux arcs de cercle : c'est la médiatrice
du segment [AB].
5_4 espace et géométrie.odt clicprof.free.fr 12/13

3
3Définir les hauteurs d'un triangle Définir les hauteurs d'un triangle
Soyons curieux
Au repos les cordes des balancelles sont alignées avec la hauteur
du triangle formé par les poteaux.
3.1) Définition
Dans un triangle, une hauteur est une droite qui passe par un sommet et qui est
perpendiculaire au côté opposé à ce sommet.
(Δ1) est la hauteur du triangle ABC issue du sommet B et (Δ2) celle issue du sommet A.
5_4 espace et géométrie.odt clicprof.free.fr 13/13