WWW.MATHS-ES.FR WWW.MATHS

WWW.MATHS-ES.FR
WWW.MATHS-ES.FR
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
MATHS-ES.FR
Terminale ES-m´ethode Chapitre 5: Int´egration
Primitives
Table des mati`eres
1 Primitives 1
1.1 Rappels ........................................... 1
1.2 Recherched’uneprimitive................................. 1
1.3 Casdel’exponentielle.................................... 2
1.4 Prouver qu’une fonction est une primitive . . . . . . . . . . . . . . . . . . . . . . . . 3
2 Primitive prenant une valeur donn´ee en un point 3
1 Primitives
1.1 Rappels
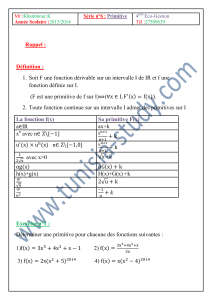
f(x) = Primitive F(x) = l’intervalle f(x) = Primitive F(x) = l’intervalle
1xR1
xln(x) ]0; +∞[
(Tous les r´eels sauf 0)
xx2
2R1 x2
−1
xR∗
x2x3
3R1 x3
−1
2x2R∗
x3x4
4R1 x4
−1
3x3R∗
x4x5
5R1 x5
−1
4x4R∗
exexReax+beax+b
aR
(aet br´eels a6= 0)
1.2 Recherche d’une primitive
rExemple 1 : Fonctions polynˆomes
fest d´efinie sur Rpar f(x) = 5x2−3x+ 1 .
D´eterminer une primitive Fde fsur R.
*Solution:
F(x) = 5 ×x3
3−3×x2 2+xest une primitive de fsur R
En effet :
F0(x) = 5 ×3x2
3−3×2x 2+ 1 = 5x2−3x+ 1 = f(x)
Chapitre 5: Int´egration Page 1/4 Maths TES

WWW.MATHS-ES.FR
WWW.MATHS-ES.FR
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
MATHS-ES.FR
Terminale ES-m´ethode Chapitre 5: Int´egration
F(x) = 5x3
3−3x2 2+ 1
rExemple 2 : Avec la fonction ln
fest d´efinie sur ]0; +∞[ par f(x) = −2
x2+3 x.
D´eterminer une primitive Fde fsur ]0; +∞[.
*Solution:
On peut ´ecrire f(x) = −2×1
x2+ 3 ×1 x
F(x) = −2×−1
x+ 3 ×ln(x) = 2 x+ 3ln(x) est une primitive de fsur ]0; +∞[.
En effet :
F0(x) = 2×(−1)
x2+ 3 ×1 x=−2 x2+ 3 ×1 x=f(x)
F(x) = 2
x+ 3ln(x)
1.3 Cas de l’exponentielle
Rappel : (eu)0=u0euo`u uest une fonction d´erivable sur un intervalle I.
Par exemple (e2x+1)0= 2e2x+1
donc F(x) = e2x+1
2est une primitive de f(x) = e2x+1 sur R.
Plus g´en´eralement. si aet bsont deux r´eels tels que a6= 0, F(x) = eax+b
aest une primitive de
f(x) = eax+bsur R.
F(x) = −e−xest une primitive de f(x) = e−xsur R.
rExemple 3 : Primitive avec exponentielle
fest d´efinie sur Rpar f(x) = 2e2−3x.
D´eterminer une primitive Fde fsur R.
*Solution:
(2 −3x)0=−3
donc F(x) = 2 ×e2−3x
−3=−2e2−3x 3est une primitive de fsur R
En effet :
F0(x) = −2×(−3)e2−3x
3=6e2−3x 3= 2e2−3x=f(x)
F(x) = −2e2−3x
3
Chapitre 5: Int´egration Page 2/4 Maths TES

WWW.MATHS-ES.FR
WWW.MATHS-ES.FR
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
MATHS-ES.FR
Terminale ES-m´ethode Chapitre 5: Int´egration
1.4 Prouver qu’une fonction est une primitive
Rappel : Fest une primitive de fsur un intervalle Isi pour tout r´eel xde I, on a F0(x) = f(x)
M´ethode
•Calculer F0(x)
•V´erifier que F0(x) = f(x)
•Conclure : Fest une primitive de fsur I
rExemple 4 : Prouver que Fest une primitive de f
Montrer que Fd´efinie par F(x) = xln(x)−xest une primitive de f(x) = ln(x) sur ]0; +∞[
*Solution:
•Calcul de F0(x)
On pose u(x) = xet v(x) = ln(x)
On a alors u0(x) = 1 et v0(x) = 1
x
F0(x) = u0(x)v(x) + u(x)v0(x)−1 = 1 ×ln(x) + x×1
x−1 = ln(x)+1−1 = ln(x) = f(x)
•On a donc F0(x) = f(x) pour tout r´eel x∈]0; +∞[
•donc Fest une primitive de fsur ]0; +∞[
2 Primitive prenant une valeur donn´ee en un point
m´ethode
•Rechercher une primitive Fde fsur I
•Les primitives de fsont de la forme G(x) = F(x) + Cavec Cconstante r´eelle.
•Si on veut que G(a) = b, ´ecrire une ´equation d’inconnue Cpuis d´eterminer C
•R´eponse : G(x) = F8x) + Cest LA primitive de fsur Itelle que G(a) = b
rExemple 5 : Primitive prenant une valeur donn´ee en un point
fest d´efinie sur Rpar f(x) = 3e−x.
D´eterminer la primitive de fsur Rs’annulant en x= 1.
*Solution:
Rappel : (e−x)0=−e−x
F(x) = −3e−xest une primitive de fsur R.
En effet :
F0(x) = −3×(−e−x) = 3e−x=f(x)
Les primitives de fsur Rsont de la forme G(x) = −3e−x+Cavec Cconstante r´eelle.
Chapitre 5: Int´egration Page 3/4 Maths TES

WWW.MATHS-ES.FR
WWW.MATHS-ES.FR
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
WWW.MATHS-ES.FR-math´ematiques en Terminale ES –chap 5 : Int´egration
MATHS-ES.FR
Terminale ES-m´ethode Chapitre 5: Int´egration
On veut G(1) = 0.
G(1) = 0
⇐⇒ −3e−1+C= 0
⇐⇒ C= 3e−1
⇐⇒ C=3
e
G(x) = −3e−x+3
eet la primitive de fsur Rtelle que G(1) = 0
Chapitre 5: Int´egration Page 4/4 Maths TES