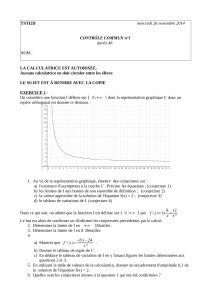
Exercice n°1 On considère les fonctions définies sur ℝ par : F(x

Intégration – Terminale – 0490 – Fonctions exponentielles – 28.08.12
http://www.soutienpedagogique.com
Exercice n°1
On considère les fonctions définies sur  par :
F(x) = (ax + b) ex et f(x) = 2x ex
Déterminer les réels a et b pour lesquels la fonction F est une primitive de la fonction f sur  .
Exercice n°2
Une entreprise fabrique des biens de grande consommation.
Le coût marginal de production de q produits exprimé en milliers d’euros, est égal à :
 q  [0 ; + ∞[ , Cm(q) = 3q + 4 + 2e−0,2q
Sachant que les frais fixes de production s’élèvent à 50 000 € et que le coût marginal représente la dérivée du
coût total, déterminer le coût total de production de q produits, noté C(q) .

Intégration – Terminale – 0490 – Fonctions exponentielles – 28.08.12
http://www.soutienpedagogique.com
Exercice n°1
On cherche les réels a et b tels que F soit une primitive de f , c’est-à-dire pour que f soit la dérivée de F .
La fonction F est le produit d’un polynôme et de la fonction exponentielle, toutes deux dérivables sur  ; F est
donc dérivable sur  .
F est de la forme uv , avec, pour tout réel x :
• u(x) = ax + b
• v(x) = ex
On en déduit : F’ = u’ v + u v’ , avec pour tout réel x :
• u’(x) = a
• v’(x) = ex
On obtient finalement :
 x   , F’(x) = aex + (ax + b) ex
Soit : F’(x) = (ax + b + a) ex
On en déduit : F’ = f  ax + b + a = 2x
Or, deux polynômes sont égaux si et seulement si les coefficients de leurs termes de même degré sont égaux :
a = 2
b + a = 0
a = 2
b = − 2
Finalement, la fonction F(x) = (2x − 2) ex est une primitive de f sur .

Intégration – Terminale – 0490 – Fonctions exponentielles – 28.08.12
http://www.soutienpedagogique.com
Exercice n°2
Si le coût marginal représente la dérivée du coût total, le coût total est alors une primitive du coût marginal.
On recherche donc une primitive de Cm sur [0 ; + ∞[ . Cm est de la forme u + v , avec :
• u(q) = 3q + 4
• v(q) = 2e−0,2q
Or, sur [0 ; + ∞[ :
• une primitive de u est U(q) = 3
+4q
• une primitive de v est V(q) = − 10e−0,2q
Les primitives de la fonction Cm sur [0 ; + ∞[ sont donc de la forme, pour k réel quelconque :
Ck(q) = 3
+ 4q − 10e−0,2q + k
On sait par ailleurs que les frais fixes de production s’élèvent à 50 000 € : cela signifie que le coût total de
production de 0 produit est égal à 50 000 € .
Finalement, la fonction de coût total C vérifie :
• Il existe k   tel que  q  [0 ; + ∞[ , C(q) = 3
 + 4q − 10e−0,2q + k
• C(0) = 50 (et non pas 50 000 car les coûts sont exprimés en milliers d’euros)
A partir de l’expression de C , on déduit que C(0) = − 10e0 + k = − 10 + k − 10 + k = 50  k = 60
Le coût total de fabrication de q (≥ 0) produits, exprimé en milliers d’euros, est donc :
C(q) = 3
+ 4q − 10e−0,2q + 60