09. Racines carrées - copie

A 1
A 2
A 3
A 4
A 5
A 6
A 7
A 8
A 9
O
1
1
1
1 1
1
1
1
1
Ch IX RACINES CARREES
1. Définition. Symbole. Nombre irrationnel
A) Carré et racine carrée
Le nombre noté
a
est le nombre positif dont le carré redonne a.
Le symbole s’appelle le radical.
L'opération "carré" et l'opération "racine carrée" sont des opérations contraires.
B)
0=0
;
1=1
;
9=3
;
(−8)
n’existe pas
1,44 =1,2
;
4
9
=
2
3
;
4
9
=
2
9
; 2
7
3
La racine carrée d'un nombre négatif n'existe pas.
C) Je retiens
2
⎛
⎝⎞ ⎠
2
= 2
7
⎛
⎝⎞ ⎠
2
= 7
1, 8
⎛
⎝⎞ ⎠
2
= 1,8
a
⎛
⎝⎞ ⎠
2
= a (a étant positif)
32
= 3
102
= 10
4, 62
= 4,6
a2
= a
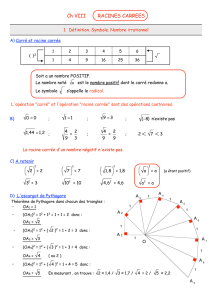
D) L'escargot de Pythagore
Théorème de Pythagore dans chacun des triangles :
• OA1 = 1
• (OA2)2 = 12 + 12 = 1 + 1 = 2 donc :
OA2 =
2
• (OA3)2 = 12 + (
2
)2 = 1 + 2 = 3 donc :
OA3 =
3
• (OA4)2 = 12 + (
3
)2 = 1 + 3 = 4 donc :
OA4 =
4
( ou 2 )
• (OA5)2 = 12 + (
4
)2 = 1 + 4 = 5 donc :
OA5 =
5
En mesurant , on trouve :
2
≈ 1,4 /
3
≈ 1,7 /
4
= 2 /
5
≈ 2,2
( )2
1
2
3
4
5
6
( )2
1
4
9
16
25
36

2. Equation x2 = a
x2=−14
pas de solution
x2=0
x = 0
S=0
{ }
x2=9
x = 3 ou x = - 3
S=−3 ; 3
{ }
x2=7
x =
7
ou x = -
7
S=−7 ; 7
⎧
⎨
⎩
⎫
⎬
⎭
si a < 0 alors
S=
{ }
Je retiens
x2=a
si a = 0 alors
S=0
{ }
si a > 0 alors
S=−a ; a
⎧
⎨
⎩
⎫
⎬
⎭
3. Multiplier des racines carrées
A) Avec la calculatrice
2×3
6
= 1 donc
2×3
=
6
B) Démontrons que
2×3
=
6
( pour ceux qui sont intéressés )
— Soit N =
2×3
. N est un nombre positif.
— Calculons
N2
N2
=
2×3
⎛
⎝⎞ ⎠
2
N2
=
2×3
⎛
⎝⎞ ⎠×2×3
⎛
⎝⎞ ⎠
N2
=
2×2
x
3×3
N2
= 2 x 3
N2
= 6 N est positif donc :
N =
6
Finalement
2×3
=
2 x 3
Je retiens si a et b sont positifs alors
a×b
=
ab

C) Calculs
•
2×18
=
36
•
5×2
=
10
•
3 2 ×5 7
= 3 x 5 x
2
x
7
= 6 = 15 x
14
= 15
14
•
3 6
⎛
⎝
⎜ ⎞
⎠
⎟
2
=
3 6
⎛
⎝
⎜ ⎞
⎠
⎟ ×3 6
⎛
⎝
⎜ ⎞
⎠
⎟
•
−4 6
⎛
⎝
⎜ ⎞
⎠
⎟
2
=
−4 6
⎛
⎝
⎜ ⎞
⎠
⎟ × −4 6
⎛
⎝
⎜ ⎞
⎠
⎟
= 3 x 3 x
6
x
6
=
−4× −4
( )
×6×6
= 9 x 6 = 16 x 6
= 54 = 96
4. Diviser deux racines carrées
A) Avec la calculatrice
6
2
–
3
= 0 donc
6
2
=
3
B) Démontrons que
6
2
=
3
( pour ceux qui sont intéressés )
D' après précédemment, on a :
6
=
2×3
donc
6
2
=
3
Je retiens si a et b sont positifs (b≠0) alors
a
b
=
a
b
C) Exemples
18
2
=
18
2
!
100
5
=
100
5
=
9
=
20
= 3
5. Simplifier une racine carrée
A) Exemple
18
=
9×2
!=
9×2
On a simplifié
18
=
3 2
(sous le radical, le nombre est plus petit qu'au départ)

B) Je retiens le procédé
50
=
25 ×2
!
50
=
10 ×5
! = 5
2
! = ?! ! !
A gauche, on peut simplifier grâce à
25
= 5. Il faut utiliser les carrés des nombres entiers :
4 ; 9 ; 16 ; 25 ; 36 ; 49 ; 64 ; 81 ; 100 ; 121 ; 144 ; 169 ; 196 ; 225 . . .
C) Remarque : on peut aussi faire
50
=
10 ×5
! =
2×5×5
!=
2×5
!=
5 2
mais c’est plus long !
6. Additionner ou soustraire des racines carrées
A) Contre -exemple
9+16 ≠25
ATTENTION :
a+b≠a+b
3 + 4 ≠ 5 et
a−b≠a−b
B) Réduire des sommes où il y a des nombres irrationnels
A =
3 2 +5 2 −2 2
= ( 3 + 5 – 2 ) x
2
= 6 x
2
=
6 2
On réduit comme pour :
3x + 5x – 2x
B =
7 3 +2 5
B ne se réduit pas comme :
7x + 2y
C =
7 3 +275
=
7 3 +2×25 ×3
=
7 3 +2×5×3
=
7 3 +10 3
=
17 3
7. Quotients avec dénominateur irrationnel
A =
3
5
=
3×5
5×5
=
3 5
5
=
3
5
5
B =
15
2 3
=
15 ×3
2 3 ×3
=
15 3
6
=
5 3
2
Quand il y a une racine carrée au
dénominateur d'un quotient, on
peut la faire disparaître de ce
dénominateur.