Les Nombres Décimaux

Chapitre 1
Les Nombres Décimaux
1. Numération de position
a) Rang des chiffres
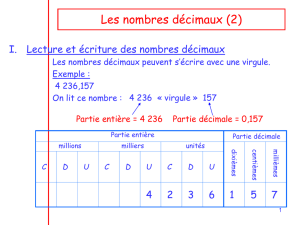
Exemple : 3 857,926
Millions
Centaines de milles
Dizaines de mille
mille
Centaines
dizaines
unités
dixièmes
centièmes
millièmes
Dix millièmes
Cent millièmes
millionièmes
3
8
5
7,
9
2
6
Partie entière Partie décimale
Dans ce nombre :
 Bien que 3 soit inférieur à 8, la valeur du chiffre 3 est supérieur à celle du chiffre 8 (3 est le chiffre des
milliers et 8 le chiffre des centaines).
 Ce nombre contient 3 857 926 millièmes ; 3 857 unités ; 385 dizaines.
Attention aux « 0 » inutiles : 3,060 03,3 14,0 103 400
n°16 page 15, n°17, n°18, n°19, n23 et n°20, n°87, n°88, n°100.
b) Nombres entiers et nombres décimaux
Exemples de nombres entiers : 0 ; 2 ; 8 ; 128
Exemples de nombres décimaux : 2,3 ; 5,72 ; 123,123 ; 2 ; 8 ; 0
Remarques importantes :
Un nombre entier est un nombre décimale (sa partie décimale est égale à zéro).
Le résultat de la division de 4 par 3 est environ égal à 1,333…….. Ce résultat n’est pas un nombre décimal car la
division ne s’arrête pas.
2. Ecritures d’un nombre décimale
Rappel : Une fraction est un quotient de deux nombres entiers.
a) Fraction décimale
Définition : Une fraction décimale est une fraction dont le dénominateur est égal à 10, 100, 1 000, ….
En lettres
Un
dixième
Un
centième
Un
millième
Douze
centièmes
Vingt-trois
millièmes
Deux cent six
dixièmes
Fraction
décimale
Ecriture
décimale
0,1
0,01
0,001
0,12
0,023
20,6

b) Différentes écritures
Ecriture décimale : 453,51
En lettres : 453 unités, 5 dixièmes et 1 centième ou 453 unités et 51 centièmes.
3. La demi-droite graduée
Sur une demi-droite graduée, un point est repéré par un nombre appelé abscisse.
On dit que l’abscisse de A est 3 et on note : A(3).
Exemples : Quelles sont les abscisses de B et C ?
Place les points D et E d’abscisses respectives 5,5 et 2,5.
4. Comparer et ranger les nombres
a) Comparer
Comparer deux nombres, c’est dire s’ils sont égaux ou dire lequel des deux est supérieur à l’autre.
Pour cela, on utilise les symboles : < : « … est inférieur à … »
> : « … est supérieur à … »
Exemple : 8,32 < 8,4
32 et 4 n’occupent pas le même rang. (8,4 = 8,40)
b) Ranger
Ranger des nombres dans l’ordre croissant, c’est les ranger du plus petit au plus grand.
Exemple : Range : 3 ; 2,31 ; 2,5 ; 1,9
Ranger des nombres dans l’ordre décroissant, c’est les ranger du plus grand au plus petit.
Exemple : Range : 9,6 ; 8,9 ; 11 ; 8,79.

5. Encadrements et valeurs approchées
Encadrer un nombre, c’est l’écrire entre un nombre qui lui est inférieur et un nombre qui lui est supérieur.
Exemple : Encadre le nombre 33,486 à l’unité, au dixième puis au centième et dans chaque cas donne la valeur
approchée par excès et par défaut.
Encadrement à l’unité : 33 < 33,486 < 34
Valeur approchée par défaut : 33
Valeur approchée par excès : 34.
Le plus : 33 est l’arrondi à l’unité.
Encadrement au dixième : 33,4 < 33,486 < 33,5.
Valeur approchée par défaut : 33,4
Valeur approchée par excès : 33,5.
Le plus : 33,5 est l’arrondi à l’unité.
Encadrement au centième : 33,48 < 33,486 < 33,49
Valeur approchée par défaut : 33,48
Valeur approchée par excès : 33,49
Le plus : 33,49 est l’arrondi à l’unité.