math 30421 Module 3 dérivées partie 2 avec exercices

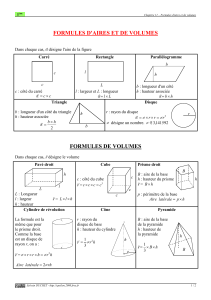
Module 3 (12 cours) Partie 2
LE NOMBRE 2 – LES OPÉRATIONS
Dérivées
Chapitre 5 – Calcul différentiel

Applications de la dérivée
5.1 Taux de variation instantané
En physique
La vitesse instantanée
x dx

t  0 t
dt
v  lim
; où x représente la position et t le temps. V = x’(t)
Ex : Du haut d’un pont, une pierre est lancée verticalement vers le haut. La position x de la pierre au-dessus
de la rivière, en fonction du temps t, est donnée par x(t) = 58,8 + 19,6t - 4,9t2, où t est en secondes et x(t),
en mètres.
a) Déterminons la fonction donnant la vitesse
de la pierre en fonction du temps.
V(t)  x' (t)  19,6  9,8t , en m/s
b) Calculons la vitesse initiale de la pierre.
f) Déterminons la hauteur du pont duquel est
projetée la pierre.
x(t)  58,8  19,6t - 4,9t2 , au temps t = 0
x(0)  58,8  19,6(0)- 4,9(0)2  58,8 en m.
V(0)  19,6  9,8(0)  19,6 , en m/s
g) Déterminons la distance totale parcourue
par la pierre, du point de lancement jusqu’à
la rivière.
c) Déterminons le temps nécessaire pour que
la pierre cesse de monter.
Elle part de 58,8m se rend à 78,4m
et se rend à nouveau à 0m.
V(t)  19,6  9,8t  0
19,6  9,8t
78,4  58,8  78,4  98 en m.
t  2 , en secondes
d) Calculons la vitesse de la pierre après 3
secondes.
V(3)  19,6  9,8(3)
h) Déterminons la vitesse de la pierre au
moment précis où elle touche l’eau.
x(t)  58,8  19,6t - 4,9t2  0
V(3)  9,8 , en m/s
t
e) Déterminons la hauteur maximale
qu’atteindra la pierre.
t
x(t)  58,8  19,6t - 4,9t2 au temps t = 2 s.
x(2)  58,8  19,6(2)- 4,9(2)  78,4 en m.
2
t
V(t)  19,6  9,8t
 b  b 2  4ac
2a
V(6)  19,6  9,8(6)
 19,6  (19,6) 2  4(4,9)(58,8)
V(6)  39,2 , en m/s
2(4,9)
 19,6  39,2
 t 1  2  t 2  6
2(4,9)
Page 1
L’accélération instantanée
v dv

t  0 t
dt
a  lim
; où v représente la vitesse et t le temps. A = v’(t) = x’’(t)
Ex : La vitesse d’une particule dans une direction donnée varie en fonction du temps selon l’expression
suivante, en m/s :
v(t)  45  10t  5t2
a) Déterminons l’accélération moyenne sur [0s, 3s].
A 0 ,3 
V(3)  V(0) 30  45  15
2


 5 en m/s
30
3
3
b) Déterminons l’accélération instantanée à t = 2s.
A(t)  V' (t)  10  10t
A(2)  10  10(2)  10 en m/s2
c) Représentons graphiquement la courbe v ainsi que la sécante et la tangente précédente.
P
t
Exercice 5.1 p. 175 # 1, 2, 3
Page 2
En chimie
La notion de taux de variation instantanée est utilisée dans l’étude d’une réaction chimique.
Ex : Deux produits chimiques, A et B, réagissent pour former un produit
La quantité du produit C en fonction du temps est noté Q(t).
Soit Q(t)  2 
C : AB  C
30
; où t  0s,60s  et Q(t) est en grammes.
2t  15
a) Déterminons la fonction T donnant le taux de variation instantané de la quantité du produit C en
fonction du temps t.
T(t)  Q' (t)  0 
0(2t  15)  30(2)
2t  15
2

60
2t  152
, en g/s
b) Calculons la quantité initiale du produit C et le taux de variation initial.
Q(0)  2 
30
30
2
 22 0
2(0)  15
15
T(0) 
60

2(0)  15
2
60
 0,27 en g /s
225
c) Déterminons approximativement, à l’aide des représentations graphique de Q et de T.
i)
le taux de variation instantané lorsque Q = 1,4g.
ii) la quantité lorsque le taux de variation instantané est de 0,1g/s.
Q(t)
T(t)
t
t
d) Calculons algébriquement :
Q(t)  2 
2  1,4 
30
 1,4
2t  15
30
2t  15
0,6(2t  15)  30
2t  15  50
T (t) 
60
2t  152
 0,1
60
2
 2t  15 
0,1
600  2t  15
2
600  2t  15
2t  35
2t  24,495  15  9,495
t  17,5 en secondes
t  4,7 en secondes
T(17,5) 
60
 0,024 g / s
217,5  15 2
Q( 4,7)  2 
30
 1,72g
24,7   15
e) Interprétons les graphiques de Q et T.
Q augmente rapidement au début et lentement à la fin et T diminue rapidement au début et lentement à la fin.
Page 3
En géométrie
Ex : Soit un ballon de forme sphérique dont l’aire A et le volume V varient en fonction du rayon r, où r est en
centimètres.
a) Déterminons la fonction TA, donnant le taux de variation instantané de l’aire de la sphère en fonction
du rayon r.
Ta (r)  A'(r)  8r exprimé en cm2/cm
A(r)  4r2
b) Déterminons la fonction Tv, donnant le taux de variation instantané du volume de la sphère en fonction
du rayon r.
V(r) 
4 3
r
3
Tv (r)  V'(r)  4r2 exprimé en cm3/cm
En économie
Nous pouvons définir la fonction Cm(q), donnant le coût marginal instantané.
C dC

 C'(q)
q  0 q
dq
Cm (q)  lim
Ex : Soit une compagnie dont les coûts totaux de production en fonction de la quantité sont donnés par
C(q)  q  2000 , où q désigne le nombre d’unités produites q  0,300  et C(q) désigne les coûts totaux en
dollars.
a) Déterminons la fonction donnant le coût marginal instantané en fonction de la quantité q.
C'(q) 
1 21
1
q 0 
, en $/unité
2
2 q
b) Évaluons le coût marginal pour q = 1 et q = 100.
C'(1) 
1
2 1
C'(100 ) 

1
, en $/unité
2
1
1

 0,05 , en $/unité
2 100 20
c) Déterminons les coûts totaux lorsque le coût marginal instantané est de 0,03$/unité.
C'(q) 
1
2 q
 0,03
1
 q
2(0,03)
q  277,8 , environ 278 unités.
Page 4
Nous pouvons définir la fonction Rm(q), donnant le revenu marginal instantané. R m (q)  lim
q0
R dR

 R ' (q)
q dq
Ex : Soit une compagnie dont les revenus en fonction de la quantité sont donnés par R(q) 
2q3  50 q2
q2  1
où q désigne le nombre d’unités vendues, q  0,100 , et R(q) désigne les revenus totaux en dollars.
a) Déterminons la fonction Rm, donnant le revenu marginal instantané en fonction de la quantité q.
R'(q) 
R'(q) 
(6q2  100 q)( q2  1)  (2q3  50q2 )(2q)
q
2
 1
2
6q4  6q2  100 q3  100 q  4q4  100 q3
q
2
 1
2

2q4  6q2  100 q
q
2
 1
2
, $/unité
b) Évaluons le revenu marginal pour q = 2 et q = 5.
R'(2) 
R'(5) 
2(2) 4  6(2)2  100(2)
(2)
2
 1
2
2(5) 4  6(5)2  100(5)
(5)
2
 1
2
 10,24 , $/unité
 2,002 , $/unité
Le profit P d’une entreprise est donné par la différence entre les revenus et les coûts. P(q) = R(q) – C(q). Le
profit est maximal lorsque R’(q) = C’(q), ou P’(q) = 0.
Ex : Soit R(q) et C(q) définis par les fonctions de la quantité q. R(q)  13q et C(q)  q2  22 , où q désigne le
nombre d’unités en milliers produites, q  0,12, R(q) désigne les revenus en milliers de dollars et C(q), les
coûts en milliers de dollars.
a) Déterminons la fonction qui donne le profit en fonction de la quantité q.
P(q)  R(q)  C(q)  13q  (q2  22)  q2  13q  22
b) Évaluons le profit (perte) lorsque q = 1, q = 5 et q = 11.
P(q)  q2  13q  22
P(1)  (1)2  13(1)  22  10 , donc une perte de 10000$
P(5)  (5)2  13(5)  22  18 , donc un profit de 18000$
P(11)  (11)2  13(11)  22  0 , donc aucun profit.
c) Déterminons une valeur de q qui peut maximiser le profit et
représentons graphiquement les courbes correspondantes.
P' (q)  2q  13  0
 2q  13
q  6,5
d) Évaluons le profit maximal.
q
P(6,5)  (6,5)2  13(6,5)  22  20,25 , donc 20250$
Exercice 5.1 p. 175 # 4, 5, 6, 7, 8, 9, 10
Page 5
5.2 Taux de variation liés
Lorsque nous avons une fonction, par exemple, z = f(x), il arrive fréquemment que la variable x soit elle-même
fonction d’une autre variable, par exemple x = g(t). Dans ce cas, z est également fonction de t.
Pour déterminer le taux de variation instantané de z par rapport à t, c’est-à-dire dz/dt, il suffit d’utiliser la
règle de dérivation en chaîne. dz/dt = dz/dx x dx/dt.
Ex. 1 : Nous gonflons un ballon sphérique, dont le volume en fonction du rayon est donné par V(r)  4  r 3
3
Sachant que le rayon de ce ballon en fonction du temps est donnée par r(t)   5t  60t , où r est en
2
7
centimètres, t, en secondes et 0 s  t  6 s :
7
a) déterminons la fonction donnant le taux de variation du volume par rapport au temps, soit
/dt.
dV dV dr


dt
dr dt
4
 r3
3
V(r) 
dV
dV
  10t 60 
 4 r 2 


dt
7 
 7
b) Évaluons
dV
/dt lorsque t = 1s.
dV
  10t 60 
 4 r 2 


dt
7 
 7
t  1s
r(1) 
 5(1) 2 60(1) 55


7
7
7
2
3
dV
 55    10(1) 60 
 4   

  1763,85 cm /s
dt
7 
 7   7
c) Évaluons dV/dt lorsque r = 25 cm.
r (t ) 
 5t 2 60t

 25
7
7
 5t 2  60t  175
dV
  10t 60 
 4 r 2 


dt
7 
 7
dV
60  25000 cm3/s
2   10(5)
 4 25 


dt
7 
7
 7
5t 2  60t  175  0
t
t
 b  b 2  4ac
2a
60  60 2  4(5)(175)
2(5)
 t  7s  t  5s on rejette le 7s car il n’appartient pas à l’intervalle.
Ex. 2 : Le volume d’un cube dont l’arête est en centimètres, s’accroît à un rythme de 300 cm 3/min. Soit x,
l’arête en cm et V le volume en cm3 du cube. Quel est le taux de variation de l’arête lorsque le volume est 512
dV dV dx
cm3?


dt
3
V  x  512  x  8
dx
dt
300  3x 2
dx
dt
dV
 300cm3 / min
dt
dx 300 100

 2
dt 3x 2
x
dx
?
dt
dx
dt
V 512

100 100 25 en


64 16
(8) 2
cm/min.
Page 6
Ex. 3 : Chantal est sur le quai d’une gare, en C, à 30m d’un point A d’une voie ferrée. Un train T s’éloigne de A
à une vitesse de 35 km/h. Évaluons le taux de variation instantané de la distance séparant Chantal du train,
lorsque le train est à 50 m de celle-ci.
x
A
T
Soit x, la distance en km de A à T,
z, la distance en km de C à T.
D’après la relation de Pythagore,
0,03
m
z
z2  x2  (0,03)2
Chantal
Si la vitesse du train est de 35 km/h, donc dx  35
dt
dz
?
dt
z2  x2  (0,03)2 , on doit dériver par rapport à t.
z  50m  0,05 km , donc
2z
0,052  x2  (0,03)2
dz 2x dx x dx x


 (35)
dt 2z dt z dt z
x2  0,0025  0,009  0,0016
dz
dt
dz
dx
 2x
0
dt
dt
k 0 ,05 km

0,04
(35)  28 en km/h.
0,05
x  0,04 , on rejette le -0,04
Ex. 4 : On remplit d’eau, au rythme de 15 cm3/s, un filtre à café en forme de cône. Le cône a un rayon de 6 cm
et une hauteur de 8 cm.
a) Déterminons le taux de variation instantané de la hauteur h par rapport au temps, lorsqu’il y a 4 cm
d’eau dans le cône.
Dans un cône, il y a deux variables qui varient, il faut toujours remplacer le h en r ou le r en h, dépendant celle
qu’on dérive par.
V(r , h) 
1 2
r h
3
V(h) 
3
h3
16
dV
 15cm3 / s
dt
dV dV dh 9
dh


h2
dt dh dt 16
dt
dh
?
dt
9
dh
15 
h2
16
dt
On sait aussi r  6 on veut dériver h
h 8
15  16 dh

dt
9h2
2
r
3h , alors
1  3h 
3
V(h)    h 
h3
4
3  4 
16
dh
dt
h 4

r=6cm
h=8cm
15  16
5 cm/s

9(4) 2 3
h  4cm
Page 7
b) Déterminons le taux de variation instantané du rayon r par rapport au temps lorsqu’il y a 4 cm d’eau
dans le cône.
V(r , h) 
1 2
r h
3
V(h) 
4 3
r
9
dV
 15cm3 / s
dt
dV dV dr 4 2 dr

 r
dt
dr dt 3
dt
dr
?
dt
4
dr
15   r 2
3
dt
On sait aussi r  6 on veut dériver h
h 8
15  3 dr

dt
4 r 2
h
8r 4r , alors
1
 4r  4

V(r)   r 2     r 3
6
3
3
3 9
dr
dt
h 4

r=6cm
h=8cm
45
5 cm/s

4 (3) 2 4 
h  4cm
4
4r
 r  3cm
3
Exercice 5.2 p. 182 # 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Page 8
Problèmes d’optimisation
Ex. 1 : Une sauveteuse dispose de 200 m de corde et de quelques bouées pour
délimiter une aire rectangulaire destinée à la baignade dans un lac. La plage
formera l’un des côtés du rectangle, et la corde formera les trois autres côtés.
T
Détermine les dimensions qui maximiseront l’aire réservée à la baignade.
a) S’il n’y a aucune restriction.
Soit A, l’aire de la région,
l, la largeur,
L, la longueur.
Avec 200m de corde
1L  2l  200
Nombre critique
si l  50
A' l   0
A  Ll
A  l   200  2l  l
1L  2l  200
200  4l  0
A  l   200l - 2l2
1L  2  50   200
4l  200
L  100
l  50
L’aire réservée à la baignade serait au maximum lorsque la largeur serait de 50m et la longueur de 100m.
b) Si l’aire de baignade ne peut pas s’étendre à plus de 40 m de la plage en raison de la profondeur de
l’eau.
si l  40
1L  2l  200
1L  2  40   200
L  120
L’aire réservée à la baignade serait donc de 40m et la longueur de 120m.
Exemple 2 – Une boîte de carton dont la base est carrée a un volume de 8 litres.
a) Détermine les dimensions qui vont minimiser la quantité de carton nécessaire à sa
fabrication.
La quantité représente l’aire totale.
1L  1000cm3
V  x xh
8000  x h
2
Atotale  2x2  4xh
J’ai besoin de dériver la formule de l’aire, mais il faut y avoir juste une variable, donc je vais isoler une des
variables de la formule du volume.
8000  x2h
8000
h
x2
8000
Atotale  2x2  4x 
x2
32000
Atotale  2x2 
x
32000
A'totale  4x 
x2
nombre qui donne l'aire minimale
4x3  32000
0
x2
32000  4x3
8000  x
3
x  20
si x  20
h
8000
20 
2
 20
La dimension qui donnerait l’aire minimale est de 20 cm par 20 cm par 20 cm, donc un cube.
Page 9
b) Le carton pour la boîte coûte 0,1¢/cm2, mais le carton du fond est plus épais, et il est trois fois
plus cher. Détermine les dimensions qui vont minimiser le coût du carton.
Le coût total de la boite serait :
Atotale  dessous  dessus  4 côtés
8000
C(x)  0,3x  0,1x  0,1  4xh   h 
x2

8000 
C(x)  0, 4x2  0,1  4x 

x2 

 32000 
C(x)  0, 4x2  0,1 

 x 
2
2
Pour connaître la valeur de x qui
minimise le coût,

C(x)  0, 4x2  0,1 32000x 1

3200
x2
3200
0  0,8x 
x2
0,8x3  3200
0
x2
C'(x)  0,8x 
8000  x2h
0  0,8x3  3200
3200  0,8x
x3  4000
x  15,87
3
h
h
8000
x2
8000
15,87 
2
h  31,76
La dimension qui donnerait le coût minimal est de 15,87cm par 15,87 cm par 31,76 cm.
Page 10
Exercices supplémentaires :
1. La hauteur, h, d’une balle lancée dans les airs il y a t secondes est donnée par la fonction
h(t)  4,9t2  19,6t  2 . Détermine la hauteur maximale de la balle. (h = 21,6m)
2. Détermine les deux nombres entiers dont la somme est 20 et dont le produit est maximal. (10 et 10)
3. À la société GP, le nombre de bidules qu’une personne produit par jour est défini par
N(t)  0, 05t2  3t  5 , où t représente le nombre d’années d’expérience de la personne et
0  t  40 . Combien d’années d’expérience sont nécessaires pour maximiser la productivité? (t = 30)
4. On a 1200 m de clôture pour créer un enclos rectangulaire divisé en trois parties parallèles.
a)
Détermine l’aire maximale de l’enclos. (A = 45000m2)
b) Explique en quoi l’aire maximale changerait si chacun des côtés de l’enclos devait mesurer au
moins 180 m de longueur. (A = 43200m2)
5. On a 60 m de clôture pour construire deux enclos qui ont un côté commun. L’un des enclos doit être
carré; l’autre, rectangulaire. Détermine les dimensions qui maximisent leur aire combinée. (10m x
15m)
6. La salle d’exposition d’une concession automobile sera rectangulaire. L’arrière et les côtés du
bâtiment seront en briques et la devanture, en verre. L’aire du plancher de la salle d’exposition
mesurera 500 m2. Si la brique coûte 1200$/m et que le verre coûte 600$/m, quelles dimensions
minimisent le coût de la salle d’exposition? (19,4m x 25,8m)
7. Une boîte cylindrique d’un avoir un volume de 1 litre. Détermine la hauteur et le rayon qui
minimiseront l’aire totale de la boîte. (h = 10,9; r = 5,4)
8. On s’apprête à fabriquer une boîte de soupe de 500 cm3. Le matériau utilisé pour le dessus coûte
0,04$/cm2, tandis que celui du dessous et des côtés coûte 0,02$/cm2. Détermine les dimensions qui
minimiseront le coût. (r = 3,76 cm)
9. Un baril cylindrique à dessus ouvert doit être fabriqué avec 1 m2 d’aluminium.
a) Indique une équation qui correspond au volume du baril en fonction du rayon.
b) Quel rayon procure le volume maximal? (r = 0,326)
c) Quel est le volume maximal si le rayon ne peut pas dépasser 0,2m? (21,6)
10. Un morceau de papier rectangulaire dont le périmètre est de 100 cm doit être enroulé de façon à
former un tube cylindrique. Détermine les dimensions du papier qui produiront un tube dont le
volume sera maximal. (16,7 cm x 33,3 cm)
Page 11
11. Un verger compte 50 pommiers, et chacun produit en moyenne 200 pommes par année. Chaque arbre
supplémentaire planté dans le verger fait diminuer de 5 le nombre moyen de pommes produites.
Quel est le nombre optimal d’arbres à planter? (45 arbres)
12. Un spectacle où l’entrée coûte 30$ attire 5000 personnes. À chaque hausse de 1$ du prix
d’entrée, il y a 100 personnes de moins. Le revenu R correspond au produit du nombre de personnes
et du prix d’entrée.
a) Soit x le nombre de hausses de 1$. Indique une équation qui exprime le revenu total en fonction
de x.
b) Indique toute restriction appliquée à x. Est-ce que x peut être négatif?
c) Détermine le prix d’entrée qui maximise le revenu. (40$)
d) Ta réponse en c) changera-t-elle si le nombre de personnes ne peut dépasser 1200? (68$)
13. Détermine l’aire du plus grand rectangle que tu peux inscrire entre l’axe des x et la courbe de la
fonction y  9  x2 . (20,8)
14. Le coût du carburant au kilomètre pour un camion qui roule à v km/h est défini par
C(v) 
v
25
.

100 v
a) Quelle vitesse engendre le plus bas coût en carburant au kilomètre? (50 km/h)
b) Suppose que la conductrice ou le conducteur reçoit 40$/h pour son travail. Quelle vitesse
occasionnera le plus bas coût, carburant et salaire compris, pour un voyage de 1000 km?
(80,6 km/h)
15. Trouve un nombre positif tel que la somme de son carré et de son inverse est minimale. (0,794)
16. On découpe un carré dans chaque coin d’un morceau d’aluminium de 60 cm sur 40 cm, puis on replie
les côtés pour former une boîte sans couvercle. Détermine les dimensions qui maximisent le
volume.
(7,85 x 44,3 x 24,3)
17. On envoie des conteneurs cylindriques en acier remplis de pétrole vers une île éloignée. La hauteur
de chaque conteneur est égale à son diamètre. Une fois les conteneurs vidés à destination, l’acier
est vendu. Le coût de transport est de 10$ le mètre cube de pétrole, et l’acier se vend 7$ le
mètre carré. Détermine le rayon du conteneur qui maximise le profit par conteneur. Ne tiens pas
compte des coûts (sauf pour le transport) ni des profits associés au pétrole. Quel est ce profit? (r
= 7/5, P = 686П/25)
Exercices récapitulatifs p. 185 # 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
Page 12