solution_pb_physique_eleves_2s_

L.F.A de Fribourg LELLOUCHE Virgile
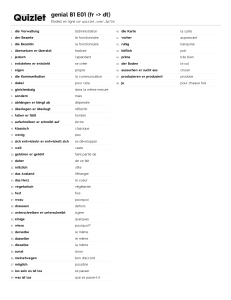
Rédiger la Solution d’un Problème en Devoir de physique (classe de 2S)
Pour chaque question exigeant un résultat numérique
1. Pour tout l’exercice, écrire les données de l’énoncé et les
convertir dans les unités SI (sauf cas particuliers: chimie (g, L...))
2. Introduire vos relations par des phrases courtes
(transitions entre 2 formules)
3. Utiliser les relations du cours en les écrivant sous forme
littérale (qui ne doit contenir que les données de l’énoncé)
4. Remplacer ensuite par les valeurs numériques converties en
unités SI (ou en faisant attention aux unités pour les cas
particuliers)
5. Faire le calcul numérique juste
6. Donner le résultat final avec l’unité convenable et son symbole
conventionnel
7. Vérifier que le résultat est correctement arrondi (nombre correct
de chiffres significatifs)
8. Encadrer ou souligner le résultat
9. Repérer un résultat aberrant et le signaler même si on est
incapable d’en trouver la cause
Exemple :
A l’arrivée d’une course de vélo, deux coureurs C1 et C2 se disputent la victoire. Le coureur C1 est à 500 m de l’arrivée et roule avec une vitesse constante de valeur v1 = 51,2 km/h. Le
coureur C2 se trouve alors à 70 m du coureur C1.
a) A quelle vitesse constante doit rouler C2 pour battre C1 sur la ligne d’arrivée ?
b) En réalité C2 roule à la vitesse constante de 60,8 km/h.
* Quel est l’intervalle de temps séparant les deux coureurs lors de leur passage sur la ligne d’arrivée ?
* Quel est, en distance, le retard du deuxième sur le premier, quand le premier franchit la ligne d’arrivée ?
Solution :
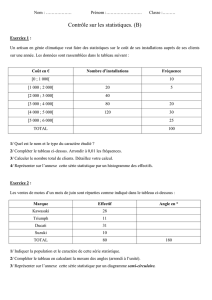
1. v1 = 51,2 km/h = 51,2 / 3,6 = 14,22222222 m/s (résultat intermédiaire à ne pas arrondir), d1 = 500 m, C2 se trouvant à 70 m derrière C1 se trouve alors à d2 = 570 m
2 ... 9. * C1, en gardant une vitesse constante, franchira la ligne d’arrivée au bout d’une durée t1 = d1 / v1 = 500*14,22222222 = 35,15625 s (résultat intermédiaire à ne pas arrondir)
* Pour franchir la ligne au même instant que C1, C2 doit posséder une vitesse (constante) de v2 = d2 / t2 (avec t2 = t1)
d’où v2 = 570/ 35,15625 = 16,21333333 m/s = 16,21333333*3,6 = 58,368 km/h soit 58,4 km/h (3 Chiffres significatifs : 3 CS comme la donnée la moins précise)
Rem : on peut retrouver ce résultat avec un « produit en crois » (règle de 3).
1. v’2 = 60,8 km/h = 60,8 / 3,6 = 16,88888889 m/s (résultat intermédiaire à ne pas arrondir)
2 ... 9. * C2 arrive en réalité au bout d’une durée t’2 = d2 / v’2 d’où t’2 = 570*16,88888889 = 33,75 s (résultat intermédiaire à ne pas arrondir)
* Puisque C1 arrive au bout de 35,15625 s, cela fait une avance de t = t’2 - t1 = 35,15625 – 33,75 = 1,40625 s = 1,41 s de C2 sur C1 (ici ce sont les décimales qui comptent et non les C.S)
ce qui fait un retard de C1 sur C2 en distance de d = v1* t = 14,22222222 *1,40 = 19,91111111 soit 19,9 m (3 Chiffres significatifs : 3 CS comme la donnée la moins précise)
Formule Littérale

L.F.A de Fribourg LELLOUCHE Virgile
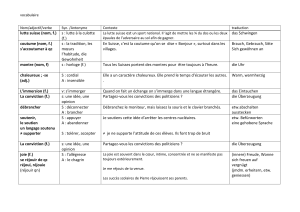
Die Lösung eines Problems in Klassenarbeit verfassen (Fach : Physik, Klasse 2S)
Für jede Frage, die ein numerisches Ergebnis
1. Für die ganze Übung, die Daten der Übung schreiben und sie in
den IS Einheiten konvertieren (außer besonderen Fällen: Chemie
(g, L...))
2. Ihre Formeln durch kurze Sätze einzuführen
(Übergänge zwischen 2 Formeln)
3. Die Formeln des Unterrichtes benutzen : sie in wörtlicher Form
schreiben
4. Danach durch die Zahlengröße ersetzen, die in IS Einheiten
konvertiert wurden (oder indem man an den Einheiten für die
besonderen Fälle aufpasst)
5. Die richtige numerische Berechnung machen
6. Das Endergebnis mit der annehmbaren Einheit und ihrem
konventionellen Symbol geben
7. Überprüfen, daß das Ergebnis richtig abgerundet wird
(erhebliche Zahlen)
8. Das Ergebnis einrahmen oder unterstreichen
9. Ein abweichendes Ergebnis entdecken und es mitteilen (nur
„impossible“ schreiben), selbst wenn man unfähig ist, davon die
Ursache zu finden
Beispiel :
A l’arrivée d’une course de vélo, deux coureurs C1 et C2 se disputent la victoire. Le coureur C1 est à 500 m de l’arrivée et roule avec une vitesse constante de valeur v1 = 51,2 km/h. Le
coureur C2 se trouve alors à 70 m du coureur C1.
a) A quelle vitesse constante doit rouler C2 pour battre C1 sur la ligne d’arrivée ?
b) En réalité C2 roule à la vitesse constante de 60,8 km/h.
* Quel est l’intervalle de temps séparant les deux coureurs lors de leur passage sur la ligne d’arrivée ?
* Quel est, en distance, le retard du deuxième sur le premier, quand le premier franchit la ligne d’arrivée ?
Lösung :
1. v1 = 51,2 km/h = 51,2 / 3,6 = 14,22222222 m/s (résultat intermédiaire à ne pas arrondir), d1 = 500 m, C2 se trouvant à 70 m derrière C1 se trouve alors à d2 = 570 m
2 ... 9. * C1, en gardant une vitesse constante, franchira la ligne d’arrivée au bout d’une durée t1 = d1 / v1 = 500*14,22222222 = 35,15625 s (résultat intermédiaire à ne pas arrondir)
* Pour franchir la ligne au même instant que C1, C2 doit posséder une vitesse (constante) de v2 = d2 / t2 (avec t2 = t1)
d’où v2 = 570/ 35,15625 = 16,21333333 m/s = 16,21333333*3,6 = 58,368 km/h soit 58,4 km/h (3 Chiffres significatifs : 3 CS comme la donnée la moins précise)
Rem : on peut retrouver ce résultat avec un « produit en crois » (règle de 3).
1. v’2 = 60,8 km/h = 60,8 / 3,6 = 16,88888889 m/s (résultat intermédiaire à ne pas arrondir)
2 ... 9. * C2 arrive en réalité au bout d’une durée t’2 = d2 / v’2 d’où t’2 = 570*16,88888889 = 33,75 s (résultat intermédiaire à ne pas arrondir)
* Puisque C1 arrive au bout de 35,15625 s, cela fait une avance de t = t’2 - t1 = 35,15625 – 33,75 = 1,40625 s = 1,40 s de C2 sur C1 (ici ce sont les décimales qui comptent et non les C.S)
ce qui fait un retard de C1 sur C2 en distance de d = v1* t = 14,22222222 *1,40 = 19,91111111 soit 19,9 m (3 Chiffres significatifs : 3 CS comme la donnée la moins précise)
wörtlicher Form
Formule Littérale