Exercices du chapitre 3

STS IRIS 2003-2004
1ère année
exercices sur le chapitre 3 : propriété des signaux.
FLEURIAULT Page 1 sur 3 747127496 14/06/17
Exercices sur le ch 3 : propriété des signaux.
Exercice 1): systèmes du premier ordre : régime transitoire avec des dipôles RLC .
Un dipôle AB est constitué de la manière suivante :
i
i1 i2
R R’
u
L C uc
1) on applique une tension u(t) aux bornes de AB :
a) établir l’équation différentielle liant uc à i2.
b) établir l’équation différentielle liant uc à u.
c) établir l’équation différentielle liant i1 à u.
2) Le condensateur étant déchargé et le circuit au repos, on applique à l’instant t = 0 une tension continue u = U.
u(t)
U
t
a) établir l’expression du courant i1(t).(trouver la fonction i1(t)).
b) établir l’expression de la tension uc(t) et en déduire l’expression du courant i2(t).
d) en déduire l’expression du courant i(t).
On rappelle que : si une fonction X(t) satisfait l'équation différentielle du premier degré suivante :
.dX + X = A où  et A sont deux constantes, alors, la fonction X(t) vaut : X(t) = A + (X(0)-A).exp(-t/) avec
dt X(0) = valeur de X(t) pour t = 0.

STS IRIS 2003-2004
1ère année
exercices sur le chapitre 3 : propriété des signaux.
FLEURIAULT Page 2 sur 3 747127496 14/06/17
Exercice numéro 2 : mesure de temps caractéristiques.
On considère un moteur à courant continu dont on sait que la vitesse  satisfait à l’équation différentielle :
 . d_ +  = k.U
dt
où U est la tension d’alimentation de l’induit, k est une constante et  est la constante de temps.
Avant l’instant référence (t = 0), le moteur tournait à la vitesse 0 = 1000 tours/min et la tension d’alimentation U
était telle que k.U = 104.7 rad/sec.
A t = 0, la tension d’alimentation U passe à une valeur telle que k.U = 157 rad / s
1. quelle est la valeur de k.U en tours / mn ?
2. quelle est l’unité de  ? (justifier)
3. donner la solution de l’équation différentielle : (t) = …
4. tracer rapidement la forme de la courbe (t).
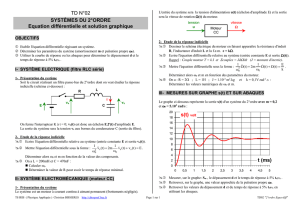
5. on a relevé la courbe (t) réelle en fonction du temps. Cette courbe se trouve dans l’annexe page suivante.
(a) donner la définition du temps de montée tm, ainsi que celle du temps de réponse à 5% tr5%. (on pourra s’aider de
dessins)
(b) mesurer sur la courbe les deux grandeurs tm et tr5%.Vous rendrez, en même temps que votre copie, la courbe 
en fonction du temps.
(c) mesurer sur la courbe la valeur de la constante de temps  en expliquant la méthode utilisée.
6. la vitesse du moteur étant de 1 = 1500 tours/min, on coupe la tension d’alimentation (U = 0)
Combien de temps devrait mettre le moteur théoriquement pour s’arrêter complètement ?
Combien de temps mettra le moteur pour descendre en dessous de la barre de  = 5% * 1500 ?

STS IRIS 2003-2004
1ère année
exercices sur le chapitre 3 : propriété des signaux.
FLEURIAULT Page 3 sur 3 747127496 14/06/17
ANNEXE : courbe (t) réelle :
Vitesse du moteur en tr/min
1000
1100
1200
1300
1400
1500
temps en sec