5Racines

5 Racines 5.1
5 RACINES
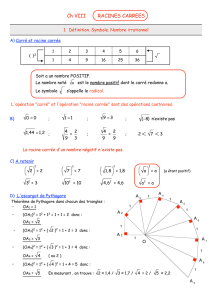
1. La racine carrée d'un nombre réel positif
On admettra que pour tout nombre réel positif, il existe un unique nombre réel
positif dont le carré est égal au nombre donné.
Définition 5.1 La racine carrée du nombre réel positif b est l'unique nombre réel positif r
dont le carré est égal au nombre b. On le note b :
rb rb=¤= 2
Le symbole est le radical et l'expression figurant sous ce symbole le
radicande.
Exemples
1) 169 13= car 13 0≥ et 13 169
2=
2) 25
95 3
=car 5
30≥et 5
325 9
2
Ê
ˈ ¯=
3) 00= car 0 0≥ et 0 0
2=
4) 11=car 1 0≥ et 1 1
2=
Remarques
1) Insistons sur le fait qu'une racine carrée est par définition un nombre réel positif.
2) On a par définition pour tout nombre réel positif : b
()
2= b et b2= b
3) Pour tout nombre réel, positif ou négatif, b2= b
En omettant la valeur absolue, on risque d'aboutir à des résultats aberrants. Par exemple :
(5-4)2 = (9-10)2 fi 5 - 4 = 9 - 10 fi 1 = -1 !!!
En fait on doit écrire : (5-4)2 = 5-4 = 1 et (9 -10)2 = 9-10 = -1 = 1
4) Il n'existe, par exemple, aucune fraction dont le carré est égal à 2 (cf les exercices). Par
conséquent 2 est un nombre irrationnel.
5) Le carré d'un nombre réel étant toujours positif, on ne peut pas définir la racine carrée d'un
nombre réel négatif.

5 Racines 5.2
6) Si b est un nombre réel strictement positif, il existe deux nombres réels opposés dont le carré est
égal à b : -b et b
7) Les calculatrices donnent une valeur exacte ou approchée de la racine carrée d'un nombre réel
positif ou nul.
8) A + B π A+B Par exemple : 7 = 9 + 16 π 9+16 = 5
2. Propriétés des radicaux
Théorème 5.2 Soit A et B deux nombres positifs.
1) A B = AB 3) A2B = AB
2) A
B = A
B si B π04)A
()
k = A
k
Exemples
1) 2 ◊5 = 10
3◊11 = 33
2) 9
25 = 9
25 = 3
5
3) 12 = 2
2◊3 = 2 23 = 23
18
25 = 18
25 = 32◊2 5 = 32 5
50 = 5
2◊2 = 5 22 = 52
2
5 = 10
25 = 10
25 = 10 5 = 1
510
36 = (33)2 = 33 = 27
73 = 7
2◊7 = 7 27 = 77
57 = 5
6◊5 = 5 65 = 535 = 125 5
23◊34◊52 = 2
2◊2◊34◊52 = 2 2◊34◊522 = 2◊32◊5◊2 = 90 2
a5 = a
4◊a = a 4a = a2a
a3b4 = a
2ab4 = a 2b4a = ab2a = ab2a
4) 2
()
5 = 2
5 = 2 4◊2 = 2 42 = 222 = 42
Remarques
1) La propriété 1 est valable pour un nombre quelconque de facteurs :
a1a2L a
n = a 1a2L an
2) Dans le cas particulier où a = 1, la propriété 2 devient : 1
b = 1 b

5 Racines 5.3
3. Le calcul avec les expressions algébriques irrationnelles
Le calcul avec les expressions irrationnelles est basé sur les propriétés des nombres réels. On utilise
par exemple l'associativité, la distributivité, les produits remarquables. Illustrons par quelques
exemples les procédés de calcul avec des expressions irrationnelles :
Exemples
1) 3 2 + 42 = 72
2) 2 3 + 45 - 33 + 25 = 65 - 3
3) 3◊215 = 615
4) 2 5 = 10
5) 8 4 = 32 = 42
6) 2 3 5 = 215
7) 3 2 ◊52 = 3◊5◊2
()
2 = 15◊2 = 30
8) 3 2 ◊28 = 3◊228 = 616 = 6◊4 = 24
9) 3 5
()
2 = 32◊5
()
2 = 9◊5 = 45
10) 2 +3
()
5 = 25 + 35 = 25 + 15
11) 3+2
()
22 = 3◊22 + 2◊22 = 62 + 24 = 62 + 2◊2 = 62 + 4
12) 8 -5
()
20 -2
()
= 160 -16 -100 +10 = 16◊10 -4-10 +10 =
410
-14 +10 = 510-14
autre méthode :
8-5
()
20 -2
()
= 22-5
()
25-2
()
= 410-4-10 +10 = 510-14
13) 5 2 -43
()
52+43
()
= 52
()
2-43
()
2 = 52◊2
()
2-42◊3
()
2 =
25 . 2 - 16 . 3 = 50 - 48 = 2
14) 2 -5
()
3-25
()
2+5
()
= 2-5
()
2+5
()
3-25
()
= (2-25) 3 -25
()
=
-23 3 -25
()
= -23 3 +46 5
15) 2 +3-8
()
2 = 2+3-22
()
2 = 3-2
()
2 = 3-26+2 = 5-26
Il y a des racin' qui s'vend' en bottes
Le radis, l'navet ou la carotte
Mais la racine que j'adore
Et qu'on extrait sans effort-eu
La racin'carrée c'est ma préférée
Boris Vian (1920-1959)

5 Racines 5.4
4. La rationalisation du dénominateur des fractions irrationnelles
Si le dénominateur d'une expression fractionnaire (numérique ou algébrique) est irrationnel, il est
souvent avantageux de transformer cette fraction en une fraction équivalente dont le dénominateur est
rationnel : on rationalise le dénominateur. Nous envisagerons deux cas :
1) Le dénominateur est un produit contenant un facteur irrationnel : on rationalise ce dénominateur
en amplifiant la fraction par ce facteur irrationnel.
2) Le dénominateur est la somme de deux expressions, dont l'une au moins est irrationnelle. On
utilise l'identité remarquable :
A+B
()
A-B
()
= A
()
2-B
()
2 = A-B
Les expressions A +B et A -B sont conjuguées. On rationalise le dénominateur en
amplifiant la fraction par l'expression conjuguée du dénominateur.
Exemples
1) 2
5 = 25
5 5 = 25 5
2) 20
35
= 20 5
355 = 20 5 15 = 45 3
3) 32
5 = 325 5 5 = 310 5
4) 2+3
5 = (2+3)5 5 5 = 10 +15 5
5) 3y
2x y = 3y y
2x y y = 3y y 2xy = 3y 2x
6) 4
3-5 = 43+5
()
3-5
()
3+5
()
= 43+5
()
32-5
()
2 = 43+5
()
9-5 = 43+5
()
4 = 3+5
7) 3
7-5 = 37
+5
()
7-5
()
7+5
()
= 37+35
7
()
2-5
()
2 = 37+35
7-5 = 37+35 2
8) y
x+y = yx-y
()
x+y
()
x-y
()
= xy
-y
x2-y
()
2 = xy
-y
x2-y
Remarque historique
La rationalisation d'un dénominateur était particulièrement importante avant l'apparition des
calculatrices. Par exemple :
1
2 = 1
1, 414213º = … (difficile) 2
2 = 1, 414213º
2 = 0,707106º (facile)

5 Racines 5.5
5. Racine n-ième d'un nombre réel
Définition 5.3 Soit x un nombre réel positif et n un nombre entier non nul. La racine n-
ième du nombre réel x, notée x
n , est le nombre réel positif défini par :
y = x
n ¤ yn= x
Le symbole
n est le radical, l'entier n l'indice, x le radicande.
Remarques
1) On dit racine cubique au lieu de racine troisième.
2) Il découle de cette définition que pour tout nombre réel positif : x
n
()
n = x
n
n = x
3) Le signe
fut introduit en 1525 par Christoff Rudolff (déformation de la lettre r, initiale du
mot racine).
Exemples
1) 81
4=3car 3 81
4=
2) 32
5=2car 2 32
5=
3) 0
n=0car 0 0
n=
4) 1
n=1car 1 1
n=
5) 3+22
=1+2car 1+2
()
2= 3+22
6) 26 +15 3
3=2+3car 2 +3
()
3= 26 +15 3
7) 1
81 2
3=car 1
21 8
3
Ê
ˈ ¯=
8) 16
625 2 5
4=car 2
516 625
4
Ê
ˈ ¯=