Mouvements de translation et de rotation

1STL-TC Date :
Mouvements de translation et de rotation
Thème du programme : Transport Sous-thème : Mise en mouvement
Type d’activités : Point cours Pré-requis : Pas de pré-requis.
Extrait BOEN :
Référentiels, trajectoires, vitesse, vitesse angulaire,
accélération.
Compétences attendues :
– Écrire et appliquer la relation entre distance par-
courue et vitesse dans un mouvement de transla-
tion à vitesse ou à accélération constante.
– Citer des ordres de grandeurs de vitesses et d’accé-
lérations.
– Écrire et appliquer la relation entre vitesse et vi-
tesse angulaire.
– Écrire et appliquer la relation donnant l’angle ba-
layé dans un mouvement de rotation à vitesse an-
gulaire constante.
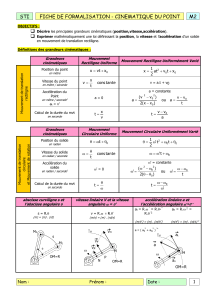
I. Vitesse et accélération
1. Notion de référentiel
On considère un train en mouvement. Paul et Virginie sont assis face à face dans le wagon.
Par rapport au sol, Paul et Virginie sont . . . . . . . . . . . . . . . .
Par rapport au wagon, Paul et Virginie sont . . . . . . . . . . . . . . . .
Un objet peut être en mouvement par rapport à un observateur
et immobile par rapport à un autre. Le mouvement d’un objet est
relatif à un objet de référence.
•L’objet, ou le point de l’objet dont on étudie le mouvement est le système étudié.
•L’objet de référence par rapport auquel on étudie le mouvement est appelé le . . . . . . . . . . . . . . . .
•Lorsque le solide de référence est lié au sol, le référentiel est appelé référentiel terrestre.
2. Vitesse
•La vitesse moyenne vmoy d’un trajet est donnée par la relation :
vmoy =d
∆t
vmoy : vitesse moyenne en mètre par seconde (m.s−1)
d : distance parcourue lors du trajet en mètre (m)
∆t: durée du trajet en seconde (s)
Si d est en kilomètre (km) et ∆ten heure (h) alors la vitesse sera exprimée en kilomètre par heure (km.h−1).
Conversion : 1 m.s−1= 3,6 km.h−1.
Application 1 : Une antilope court à une vitesse de 24,5 m.s−1, un lion à une vitesse de 80 km.h−1. Qui court le
plus vite ?

Application 2 : Au tour de France 2010, l’étape Bagnères de Luchon-Pau, longue de 187 km a été remportée par
le français Pierrick Fedrigo en 5h32min. On se propose de calculer sa vitesse moyenne lors de cette étape.
1. Exprimer en heure et par un nombre décimal, la durée de parcours de cette étape.
2. Calculer sa vitesse moyenne lors de cette étape, au dixième de km.h−1près.
3. Convertir cette vitesse en m.s−1.
•La vitesse instantanée est la vitesse à un instant donné. C’est la vitesse mesurée par les radars et indiquée
par le tachymètre de la voiture.
La vitesse instantanée v(t) à un instant t, est pratiquement égale à sa vitesse moyenne calculée pendant un
intervalle de temps très court encadrant l’instant t considéré.
Si la vitesse instantanée est constante au cours du mouvement, le mouvement est . . . . . . . . . . . . . . . .
Lors d’un mouvement uniforme d’un corps, les valeurs de la vitesse moyenne entre deux positions et de la vitesse
instantanée de ce corps, à un instant quelconque sont égales.
véhicule ou animal chameau chien scooter 50 cm3lièvre guépard F1 Airbus A380 Fusée Ariane 5
vitesse (km.h−1) 18 32 45 60 94 370 900 62300
3. Accélération
•L’accélération est une grandeur qui indique une modification affectant la vitesse d’un mouvement en fonction
du temps.
En ligne droite, pour doubler un véhicule, un motard décide d’accélérer. En 2 secondes, sa vitesse passe de v(t0)
= 87 km.h−1à v(t1) = 105 km.h−1. L’accélération correspond à la variation de vitesse du motard en 2 secondes.
1. Calculer la variation de vitesse ∆v du motard en km.h−1puis en m.s−1.
2. En déduire l’accélération du motard dans la ligne droite.
Elle correspond à la variation de la vitesse : a=v(t1)−v(t0)
t1−t0
.
véhicule auto DS3 moto routière Ariane 5 avion Rafale
accélération(m.s−2) 2,8 7 18,5 90
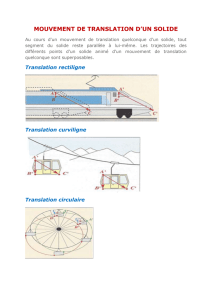
II. Mouvement de translation
1. Définition
•Un solide est en mouvement de translation si tout segment du solide reste parallèle à lui même au cours
du mouvement.
•Translation rectiligne : Tout segment du solide se déplace en restant parallèle à lui même et le mouvement
de chaque point est rectiligne. La trajectoire de chaque point est une droite.
Une voiture roulant en ligne droite est en translation rectiligne.

2. Mouvement de translation rectiligne uniforme
•Lorsque la translation est rectiligne et uniforme, la vitesse est constante au cours du mouvement et l’accélé-
ration est nulle.
La distance d parcourue par un point dans une translation rectiligne uniforme pendant une durée ∆test donnée
par la relation :
d=v×∆t
v: vitesse moyenne en mètre par seconde (m.s−1)
d : distance parcourue lors du trajet en mètre (m)
∆t: durée du trajet en seconde (s)
3. Mouvement de translation rectiligne à accélération constante
•L’accélération moyenne est donnée par la relation : a=v(t1)−v(t0)
t1−t0
.
•L’accélération moyenne peut être positive si la vitesse moyenne augmente au cours du temps ou négative si
la vitesse moyenne diminue au cours du temps.
•Lorsque l’accélération est constante, le mouvement est dit uniformément varié (accéléré si a > 0 et décéléré
si a < 0).
Lorsque le mouvement rectiligne est uniformément varié :
– la vitesse atteinte au bout d’une durée ∆test donnée par l’équation :
a=v∆t+v0v0vitesse initiale
– la distance parcourue pendant la durée ∆test donnée par l’équation :
a=1
2v∆t2+v0∆t
Application 1 : La Porsche 911 GT3 passe de 0 à 100 km.h−1en 4,1 s.
Calculer son accélération en m.s−2.
Application 2 : Au démarrage l’accélération d’une BMXS 1000RR est de 9,56 m.s−2.
1. Écrire la relation qui permet de calculer la distance parcourue en fonction du temps pour un mouvement rectiligne
uniformément accéléré.
2. Quelle distance parcourt cette moto les trois premières secondes du démarrage ?
3. Écrire la relation qui permet de calculer la vitesse en fonction du temps pour un mouvement rectiligne unifor-
mément accéléré.
4. Quelle vitesse atteint la moto au bout de 3 secondes ?
III. Mouvement de rotation autour d’un axe fixe
1. Définition
Un solide est en mouvement de rotation autour d’un axe fixe si :
– les points situés sur l’axe de rotation sont immobiles ;
– les points en dehors de l’axe décrivent des arcs de cercles centrés sur l’axe de rotation. Ils ont une trajectoire
circulaire.
Le mouvement de rotation d’un solide est caractérisé par sa vitesse angulaire ω.

2. Vitesse angulaire
La trajectoire de A est un arc de cercle de rayon OA et celle de B
un arc de cercle de rayon OB.
Pendant la durée ∆t, les deux rayons OA et OB ont tourné d’un
même angle α.
Ces 2 rayons ont donc tourné à la même vitesse angulaire ω.
ωest la vitesse de rotation du solide :
ω=α
∆t
α: angle de rotation en radian (rad)
∆t: durée du parcours en seconde (s)
ω: vitesse angulaire en radian par seconde (rad.s−1)
La distance parcourue par A est AA0= OA.αavec αen radians et celle parcourue par B : BB0= OB.α.
AA0est plus grande que BB0.
•Le mouvement de rotation est uniforme si la vitesse angulaire est constante.
Application : Les pales d’une éolienne ont une vitesse de rotation de 70 tr.min−1.
1. Calculer la vitesse angulaire de rotation en tr.s−1puis en rad.s−1.
2. De quel angle, exprimé en radian puis en degré, tourne une pale en 0,5 s ? Donnée : 360°= 2πrad.
3. Relation entre v et ω
•Le point A décrit un cercle de plus grand rayon que le point B. Le point A se déplace plus vite que le point B.
•La vitesse linéaire vd’un point d’un solide en rotation dépend de ωmais aussi de la distance R de ce point à
l’axe de rotation.
Pour le point A : vA=OA.ω et pour le point B : vB=OB.ω.
Généralisation : la vitesse linéaire vd’un point d’un solide en rotation est :
v=R.ω
v: vitesse linéaire en mètre par seconde (m.s−1)
R : distance du point à l’axe de rotation en mètre (m)
ω: vitesse angulaire en radian par seconde (rad.s−1)
Application 1 : Dans une éolienne, la vitesse ven bout de pales est de 63 m.s−1. Le rayon de balayage des pales
est de 14 m.
1. Calculer, en rad.s−1puis en tr.min−1, la vitesse de rotation des pales. Arrondir le résultat à l’unité.
2. De quel angle tourne une pale à chaque seconde ?
Application 2 : Une scie circulaire d’un diamètre de 60 cm tourne à 640 tours par minute.
1. Calculer sa vitesse angulaire en tr.s−1puis en rad.s−1.
2. Calculer la vitesse linéaire d’une de ses dents (vitesse de coupe).
3. À quelle vitesse angulaire, en tr.min−1, devrait tourner la scie pour que la vitesse de coupe soit de 30 m.s−1?