Cor2 - Jean-Romain HEU

ff:R→R
x7→ e1+cos(x2).
f
f(1) = f(−1)
x2)
∀x∈R, f(x)>0
f(R)
f(R) = [1, e2]f x 7→ x2
[0,+∞[ cos [−1,1] x7→ 1 + cos(x2)
[0,2] exp
[1, e2]
I Z∗
−
g:I7→ Z∗
−g(n) = −n+1
2
g n m I g(n) = g(m)−n+1
2=−m+1 2
n=m g
g a ∈Z∗
−n=−2a−1
a n
n∈I g(n) = −−2a−1+1
2=aZ∗
−
g
g
g a 7→ −2a−1g
g˜g:N7→ Z
∀n∈N,˜g(n) = n
2n
−n+1
2n
˜g
h:Z→N∀a∈Z, h(a) = −2a−1a < 0h(a)=2a
a>0h˜g a ∈Za < 0 ˜g(h(a)) =

˜g(−2a−1) = −−2a−1+1
2=a a >0 ˜g(h(a)) = ˜g(2a) = 2a 2= 1 ˜g◦h=IdZ
n∈Nn h(˜g(n)) = h(n/2) = 2n
2=n n h(˜g(n)) =
h(−n+1
2) = −2(−n+1 2)−1 = n h ◦˜g=IdNh= ˜g−1
R2
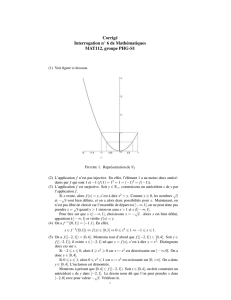
A={(x, y)∈R2|06x63 0 6y66−2x}et B={(1+cos(θ),1+sin(θ)) ; θ∈[0,2π]}.
A B
A(0,0),(3,0) (0,6) B
(1,1)
B⊂A
(x, y)B(x, y) = (1 + cos θ, 1 + sin θ)
θ∈[0,2π] cos θ>−1 sin θ>−1x>0y>0 cos θ61
sin θ61 2x+y62(1 + 1) + (1 + 1) = 6 y66−2x(x, y)
A(x, y)∈A B ⊂A
C
C={(x, y)|06x62 2 + x
26y63}.
C A B C
C A C
A(x, y) = (2,3) 0 6x62 2 + x
26y63 (x, y)∈C
6−2x= 2 < y (x, y)/∈A
B C (x, y)C(0,2) y > 2
(x, y)B(1,2) y < 2
B C
y
123x
1
2
3
4
5
6

2n+n n
n
nmod 5
2n
2n+n
n= 4,6,7
a k b =a+ 20k2b+b= 2a+a
Z/5Z2b+b= 2a+20k+a+ 20k= 2a(24)5k+a+ 5 ×(4k) = 2a15k+a= 2a+a
n2n+n
b b b = 20k+a
06a < 20 2b+b= 2a+a2b+b
b2b+b
a n 4 + 20k
6 + 20k7 + 20k13 + 20k k ∈N
n
2n+n
n
2n
2n+n
5×4 = 20
n2n2n+n
n n = 2 n= 3
2 + 6k3 + 6k
k∈N