estimation de l`erreur commise lors de l`approximation de

6
J. sci. pharm. biol., Vol.12, n°2 - 2011
POLNEAU S. & al. : Estimation de l’erreur commise lors de l’approximatio...
© EDUCI 2011.
ESTIMATION DE L’ERREUR COMMISE LORS DE
L’APPROXIMATION DE LA LOI BINOMIALE PAR LA
LOI NORMALE
POLNEAU S.1
VALLEE L.2
MALAN K.A.3
1- Département de Biostatistique, UFR des Sciences pharmaceutiques et biologiques, Université de Cocody
Abidjan, Côte d’Ivoire
2- Centre de formation professionnelle et artistique, , Abidjan, Côte d’Ivoire
3- Département de Chimie Analytique, UFR Sciences pharmaceutiques et biologiques, Université de Cocody
Abidjan, Côte d’Ivoire
- Correspondance : Sandrine POLNEAU, 18 BP 2635Abidjan 18 Côte d’Ivoire, Téléphone: [phone],
Fax:[phone], [email protected]
RESUME
Le développement de l’informatique
et des logiciels de statistique permet
actuellement l’utilisation indifférenciée
des outils de statistique classique et des
outils exacts. Les premiers sont basés sur
des approximations de lois et notamment
la loi normale tandis que les seconds
sont utilisés «hors approximation» d’où
leur qualication d’outils «exacts». Nous
nous sommes intéressés à l’étude de la
différence entre la loi binomiale «exacte» et
la loi normale «approchée». L’approximation
de la loi binomiale par la loi normale est
accompagnée d’un risque d’erreur que
nous avons quantié et nous présentons
la différence d’erreur selon la loi utilisée
dans différentes situations et comparons
les résultats dans les contextes «exact»
et «approché». Les bornes des intervalles
«exact» ou «approchée» ne différant qu’à
la troisième ou à la quatrième décimale,
l’utilisation indifférenciée des outils «exacts»
ou «approchés» est alors possible.
Mots-clés : Loi binomiale, Loi normale,
statistique exacte, Statistique approchée,
Erreur
SUMMARY
The development of the data processing
and the software of statistics currently
allows the undifferentiated use of the tools of
traditional statistics and the exact tools. The
rst are based on approximations of laws
and in particular the normal law while the
seconds are used “except approximation’’
and are then called “exact’’ tools. We were
interested in the study of the difference
between the binomial distribution “exact’’
and the normal law “approximate’’. The
approximation of the binomial distribution
by the normal law is accompanied by a risk
of error and we present the difference in
error according to the law used in various
situations and compare the results in the
contexts “exact’’ and “approached’’. The
differences of the terminals relate only to
the third or the fourth decimal. This then
authorizes the undifferentiated use of the
tools of traditional or exact statistics.
Key words: Binomial distribution,
normal law, Exact statistics, Approximate
statistics
J. sci. pharm. biol., Vol.12, n°2 - 2011, pp. 6-12
© EDUCI 2011

7
J. sci. pharm. biol., Vol.12, n°2 - 2011
POLNEAU S. & al. : Estimation de l’erreur commise lors de l’approximatio...
© EDUCI 2011.
des machines et des logiciels puissants
capables d’effectuer rapidement la plupart
des calculs que nécessitent les méthodes
exactes [Vollset 1993, Agresti 2001,
Newcombe 1998, Prum 1997]. Il convient
alors de mener la réexion sur les avantages
comparatifs de l’emploi des méthodes
approchées ou exactes.
L’objectif de ce travail a été de
quantier le risque d’erreur différentiel
lié à l’approximation de la loi binomiale
par la loi normale permettant ainsi de
vérier la validité du théorème de la limite
centrale couramment employé par les
utilisateurs d’outils statistiques dans le but
de répondre à des questions posées dans
le domaine des sciences de la santé.
INTRODUCTION
Le développement de la biostatistique
a révolutionné le traitement des données
biomédicales [Colton 1974], à l’instar de
l’épidémiologie et la santé publique pour
lesquelles cette discipline est un outil
privilégié [Bernard 1987]. Les premières
méthodes largement utilisées étaient basées
sur des hypothèses de distribution normale
des phénomènes étudiés [Schwartz 1987]
en raison de la complexité des formules de
calcul de la loi exacte.
Cependant l’approximation d’une loi
exacte (par exemple la loi binomiale) par
une loi normale est accompagnée d’une
perte d’information, et inévitablement
d’un risque d’erreur [Vollset 1993, Agresti
2001]. Or les progrès dans le domaine
de l’informatique ont mis à disposition
MATERIEL ET METHODES
LOGICIELS ET LOIS STATISTIQUES
Les logiciels employés étaient Stata 11
et Excel 2007.
Les lois statistiques ayant fait l’objet de
notre réexion étaient les lois binomiale et
normale.
M É T H O D E D ’ E S T I M A T I O N D E
L’ERREUR
Soit une variable aléatoire Y à 2
modalités notées 1 (associé au succès) et
0 (associé à l’échec) et soit la probabilité
p associée à la réalisation du succès: p =
P(Y = 1) avec 0
≤
p
≤
1 et q la probabilité
associée à la réalisation de l’échec : q =1- p
= P(Y = 0).
Alors la variable aléatoire Y suit une loi
de Bernoulli de paramètre p dont l’espérance
est égale à p et la variance à pq.
Soient n variables aléatoires
i
Y
suivant
la même loi de Bernoulli d’espérance p
et de variance pq. Considérons ensuite
la variable aléatoire X somme de ces n
variables aléatoires de Bernoulli.
Cette variable X suit une loi binomiale
dont la distribution est totalement
déterminée par la connaissance de n et
de p .
L’espérance et la variance de X répondent
aux relations suivantes : E(X)=np et
V(X)=npq.
Sous certaines conditions dépendant
des auteurs [Colton 1974, Schwartz 1987]
(par exemple pour np
≥
5 et nq
≥
5 et/ou n
grand), la loi binomiale peut être approchée
par une loi normale de même espérance et
de même variance :
[X~B(n;p)] ⇒ [X~N(np;npq)].
Pour chacune des lois ci-dessus, on
dénit d’une part la fonction de distribution
de probabilité (f(x)) et d’autre part la
fonction de répartition (F(x)). La fonction
de distribution de probabilité associe
à chacune des valeurs x prises par la
variable X sa probabilité de réalisation P(X=

8
J. sci. pharm. biol., Vol.12, n°2 - 2011
POLNEAU S. & al. : Estimation de l’erreur commise lors de l’approximatio...
© EDUCI 2011.
x). La fonction de répartition F(x)=P(X ≤ x)
associe à chaque valeur de x la somme des
probabilités des valeurs de X inférieures
ou égale à x. Ainsi F(x) =
∑
=
k
0i
P(X=i) =
P(X=0)+P(X=1)+P(X=2)+…............+P(X=x).
Nous avons utilisé dans les logiciel
Stata 11 et Excel 2007 de Microsoft
les fonctions de calcul de la distribution
de probabilité et celle de répartition
d’une variable suivant une loi binomiale
respectivement. Il s’agissait pour Stata de
« binomialp (n,k,p) et binomial(n,k,p) » et
pour Excel de « LOI BINOMIALE (k ; n ; p ;
faux) et LOI BINOMIALE (k ; n ; p ; vrai) ».
Le risque d’erreur α accompagnant la
plupart des résultats d’analyse statistique
de données biologiques est classiquement
et arbitrairement xé à 5%. C’est la raison
pour laquelle nous nous sommes intéressés
à l’étude d’un quantile particulier le
quantile à 95%. Il s’agit de trouver la
valeur de x telle que F(x)= 95%. Cependant
le caractère discret de la loi binomiale ne
permet pas de trouver dans tous les cas
une valeur entière de x qui satisfasse à la
relation : F(x)= 95%. On procède alors à un
encadrement de la fonction de répartition.
Sachant que cette fonction de répartition
est une fonction croissante on obtient alors
les relations suivantes:
x1 < x < x2
F(x1) <F(x) < F(x2)
De cet encadrement de la fonction de
répartition, nous pouvons déduire un
encadrement du risque d’erreur sans
approximation appelé risque d’erreur
« exact ».
F(x1)<F(x)<F(x2)
⇒1-F(x2)<1-F(x1)
⇔ α1<α<α2
Nous avons xé deux valeurs de p et
calculé les fonctions de répartition des lois
binomiales pour des valeurs croissantes
de n. Ces simulations nous ont permis
de représenter l’encadrement du risque
d’erreur exact pour une loi binomiale.
INTERVALLES DE CONFIANCE « EXACT »
ET « APPROCHÉ »
L’estimation ponctuelle des paramètres
complémentée par l’intervalle de conance
pour un risque d’erreur de première
espèce xé est couramment employée en
statistique. Nous avons utilisé cette seconde
méthode pour quantier l’approximation
d’une loi binomiale par une loi normale. Cet
intervalle de conance est classiquement
donné en utilisant l’approximation par la
loi Normale :
p - u1-α/2
( ) ( )
n
pp
up
n
pp
up - +
-
-
--
11
2121 aa
;
; p + u1-α/2
( ) ( )
n
pp
up
n
pp
up - +
-
-
--
11
2121 aa
;
;
Les paramètres nécessaires pour le
calcul de l’intervalle de conance exact
sont constitués par le couple (n, p).
Le nombre x est compris entre 0 et n.
Fixons n et x et faisons varier p à travers
plusieurs simulations de cas pour suivre
les positions respectives des intervalles de
conance de p «exact » et « approché ». Pour
chaque valeur de p, calculons
( )
xXP ≥
et
( )
xXP ≤
.
Cherchons deux valeurs
1
p
et
2
p
(bornes
inférieure et supérieure de l’intervalle
de confiance) telles que pour
1
p
(et
11 1pq -=
), l’on obtienne l’égalité suivante
( )
( )( ) 2
11
a==≥ ∑
=
-
n
xi
xnx
x
nqpCxXP
= α/2 que
l’on notera
( )
xG
p1
; = 1-p ; pour
2
p
(et
22
1pq -=
), l’on obtienne l’égalité suivante :
( )
( ) ( )
2
0
2
2
a==≤ ∑
=
-
x
i
xnx
x
nqpCxXP
= α/2 équivalente
à la fonction de répartition d’une loi
Binomiale que l’on notera
( )
xFp2
.
Ces probabilités
1
p
et
2
p
sont obtenues
par interpolation.

9
J. sci. pharm. biol., Vol.12, n°2 - 2011
POLNEAU S. & al. : Estimation de l’erreur commise lors de l’approximatio...
© EDUCI 2011.
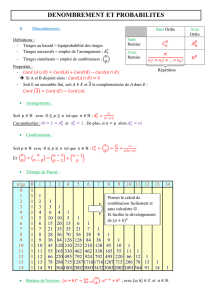
RESULTATS
Les logiciels Stata 11 et Excel 2007 ont
donné des résultats de calcul des fonctions
de distribution et de répartition identiques
avec une précision de 10 décimales.
Les calculs d’erreurs exactes déduits
par complémentarité de la fonction de
répartition étaient donc identiques à 10-10
près avec les 2 logiciels employés.
Nous estimons d’une part l’encadrement
des risques d’erreurs « exacts » présenté par
l’intervalle [α1 ; α2] autour de la valeur 5%
(gures 1 et 2) et d’autre part la différence
de résultats obtenus entre les intervalles de
conance de pourcentage p « exact » (ICe)
et « approché » (ICn) (gure 3).
Pour deux valeurs particulières de p
(p = 0,5 et p = 0,8) et des valeurs de n
croissantes par pas de 1, les encadrements
du risque d’erreur «exact» [α1 ; α2] sont
schématisés sur les gures 1 et 2. L’on
peut voir sur ces gures les uctuations
de cet encadrement autour de la valeur
théorique de 5% conventionnellement
acceptée en biologie.
Ces figures montrent une tendance
globale à la réduction de l’étendue de
l’encadrement lorsque la valeur de n
augmente. Cependant cette évolution
n’est pas linéaire, elle se fait par série.
Ainsi on aurait pu s’attendre à trouver
la relation suivante : α1
≈
α
≈
α2 pour
de grandes valeurs de n, mais les deux
valeurs α1 et α2 ne se rapprochent pas
simultanément de α. Les gures 1 et 2
montrent une évolution différente l’une par
rapport à l’autre. Concernant la gure 2,
le phénomène observé semble périodique
avec un rétrécissement progressif de
l’encadrement entrecoupé de brusques
variations.
Concernant la comparaison des calculs
d’intervalle de conance de p exact (ICe)
et approché (ICn), 3 cas de gure sont
observés selon les valeurs de p : (i) lorsque
p<0,5 : translation de ICe par rapport à ICn
vers les valeurs supérieures ; (ii) lorsque p =
0,5 : inclusion de ICn dans ICe ; (iii) lorsque
p>0,5 : translation de ICe par rapport à ICn
vers les valeurs inférieures.
Dans tous les cas, les résultats des
calculs des bornes d’intervalle de conance
de p « exact » ou « approché » ne montrent
des différences qu’au niveau de la troisième
voire de la quatrième décimale.
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110
nombre total d'observations n
a
α1
α2
5%
Figure 1 : Encadrement du risque d’erreur α pour p = 0,5

10
J. sci. pharm. biol., Vol.12, n°2 - 2011
POLNEAU S. & al. : Estimation de l’erreur commise lors de l’approximatio...
© EDUCI 2011.
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
nombre total d'observations n
a
α1
α2
5%
Figure 2 : Encadrement du risque d’erreur α pour p = 0,8
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
IC
IC "normal"
IC " exact"
n = 20
p = 0,3
np = 6
nq = 14
n = 50
p = 0,3
np = 15
nq = 35
n = 100
p = 0,3
np = 30
nq = 70
n = 10
p = 0,5
np = 5
nq = 5
n = 30
p = 0,5
np = 15
nq = 15
n = 100
p = 0,5
np = 50
nq = 50
n = 30
p = 0,8
np = 24
nq = 6
n = 50
p = 0,8
np = 40
nq = 10
Figure 3 : Intervalles de conance de pourcentage comparés sous l’hypothèse de la normalité (ICn)
et « exact » (ICe). Cas de conditions d’approximations vériées.