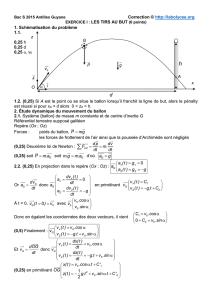
(0,25) Si A est le poi

Bac S 2015 Antilles Guyane
EXERCICE I : LES TIRS AU BUT(6 points)
1. Schématisation du problème
1.1.
0,25 h
0,25 d
0,25 , v0
1.2. (0,25) Si A est le point où se situe le ballon lorsquʼil franchit la ligne de but, alors le pénalty
est réussi si pour xA = d alors 0 < zA < h.
2. Étude dynamique du mouvement du ballon
2.1. Système {ballon} de masse m constante et de centre dʼinertie G
Référentiel terrestre supposé galiléen
Repère (Ox ; Oz)
Forces : poids du ballon,
P mg
=
les forces de frottement de lʼair ainsi que la poussée dʼArchimède sont négligés
(0,25) Deuxième loi de Newton :
.
ext
d p dv
F m
dt dt
= =
(0,25) soit
G
P m.a
= soit
G
m.g m.a
= dʼoù
G
a g
=
2.2. (0,25) En projection dans le repère (Ox ; Oz) :
0
x x
G
Z Z
a (t ) g
a
a (t ) g g
= =
= = −
Or
G
G
dv
a
dt
= donc
0
x
x
G
Z
Z
dv (t )
adt
adv (t )
a g
dt
= =
= = −
 en primitivant
1
2
x
G
Z
v (t ) C
v
v (t ) g.t C
=
= − +
À t = 0,
G
v (t ) v
= =
0
0 avec
v .cos
vv .sin
α
α
0
0
0
Donc en égalant les coordonnées des deux vecteurs, il vient
C v .cos
C v .sin
= α
+ = α
1 0
2 0
0
(0,5) Finalement :
0
0
x
G
Z
v (t ) v .cos
vv (t ) g.t v .sin
= α
= − + α
Et
G
dOG
v
dt
= donc
0
0
x
G
Z
dx(t )
v (t ) v .cos
dt
vdz(t )
v (t ) g.t v .sin
dt
= = α
= = − + α
(0,25) en primitivant
0 1
2
0 2
1
2
x(t ) v .cos .t C'
OG
z(t ) g.t v .sin .t C'
= α +
= − + α +
αx
d
z
O
k
i
v
0
h
A
P
g
G

À t = 0, OG(t )
= =
0 0
donc en égalant les coordonnées des deux vecteurs
C'
C' =
=
1
2
0
0
(0,25) Finalement les équations horaires x(t) et z(t) sont : 0
20
1
2
x(t) v .cos .t
OG
z(t) g.t v .sin .t
= α
= − + α
Pour obtenir l’équation de la trajectoire z(x) du ballon, on isole le temps t de x(t) et on reporte
l’expression de t dans z(t) :
x = v0.cos α .t donc x t
v .cos
=
α
0
et 2
0
0 0
1
2x x
z(x) g. v .sin .
v .cos v .cos
= − + α
α α
(0,25) Finalement : 2
0
. ²
( ) tan .
2. .(cos )²
g x
z x x
v
= − + α
α
2.3. (0,25) Le pénalty est réussi si pour xA = 11,0 m on a 0 < zA < 2,44 m.
2
2
0
.
tan .
2. .(cos )²
A
A A
g x
z x
v
= − + α
α
(
)
( ) ( )
2
2 2
9,81 11,0
tan55 11,0
2 11,5 cos55
A
z× = − + ×
× × = 2,1 m
(0,25)
Comme zA vérifie les inégalités 0 < zA < 2,44 m, le pénalty est réussi.
3. Étude énergétique du mouvement du ballon
3.1. (0,5 expressions + 0,5 raisonnement)
Énergie cinétique : Ec =
.m.v
2
1
2
Énergie potentielle de pesanteur : E
pp
= m.g.z
Énergie mécanique : E
m
= E
c
+ E
pp
=
.m.v
2
1
2+ m.g.z
À t = 0, le ballon est à l’origine du repère donc x = 0 et z = 0.
À cette date, l’énergie potentielle de pesanteur E
PP
= m.g.z est nulle. Seule la courbe 3 passe
par l’origine du repère du graphe des énergies. Ainsi la courbe 3 est associée à l’énergie
potentielle de pesanteur .
Les frottements étant négligés, l’énergie mécanique est constante au cours du mouvement. On
associe donc la courbe 1 à l’énergie mécanique .
La courbe 2 est donc associée à l’énergie cinétique . La vitesse diminue lors de la montée en
altitude de la balle, puis augmente au cours de la descente.

3.2. (0,25 + 0,25) Lorsque le ballon franchit la ligne de but, xA = 11,0 m ; graphiquement on lit :
EC = 28 J et EPP = 13 J.
Or EC =
A
.m.v
2
1
2 donc
C
A
E
v
m
=
2
2
soit
C
A
E
v
m
=2 en ne conservant que la solution positive.
(0,25) A v,× =
2 28
0 620
= 9,5 m.s−1.
Et EPP = m.g.zA = m.g.hA donc
PP
A
E
h
m.g
=
(0,25) soit A
h
, ,
=×
13
0 620 9 81
= 2,1 m.
Remarque : on retrouve la valeur de zA de la question 2.3.
3.3. L’énergie mécanique du ballon se conserve au cours du mouvement.
(0,25) Ainsi, entre le point O et le point A on a : Em(O) = Em(A)
soit
.m.v
2
0
1
2 + m.g.zO =
A
.m.v
2
1
2 + m.g.zA
Or zO = 0 m et zA = hA donc :
.m.v
2
0
1
2+0 =
A
.m.v
2
1
2+ m.g.hA
(0,25) En multipliant tous les termes par 2 et en les divisant par m, on obtient :
v
2
0
=
A
v
2
+ 2.g.hA
d’où :
A
v
2
=
v
2
0
– 2.g.hA
Finalement, en ne conservant que la solution positive :
A A
v v .g.h
= −
2
02
(0,25) vA =
( )
, , ,
− × ×
2
115 2 9 81 2 1
= 9,5 m.s−1.
On retrouve bien la valeur vA de la vitesse du ballon lorsqu’il franchit la ligne de but.
La conservation de l’énergie mécanique utilisée ici est confirmée.
EC = 28 J
EPP = 13 J

Bac S 2015 Antilles
EXERCICE II. SYNTHÈSE D’UN ANESTHÉSIQUE : LA BENZOCAÏNE (9 points)
1. Étude bibliographique préliminaire
1.1.
(0,5)
1.2. (0,5) La molécule de benzocaïne ne possède pas de doubles liaisons C=C, elle ne peut pas
présenter de diastéréoisomères Z/E.
De plus elle ne possède pas d’atomes de carbone asymétriques (ce qui peut impliquer des
énantiomères et/ou des diastéréoisomères selon leur nombre).
En conclusion, la molécule de benzocaïne ne présente pas de stéréoisomères de configuration
(énantiomères ou diastéréoisomères).
1.3.1. (0,5) Lors de l’étape (a) de la synthèse de la benzocaïne, un atome d’hydrogène (qui
n’apparaît pas dans l’écriture topologique) est remplacé par un groupe d’atomes NO2. Ce qui
classe cette réaction dans la catégorie des réactions de substitution.
1.3.2. (0,25) Un catalyseur est une espèce chimique qui diminue la durée d’une réaction
chimique.
Au cours de la réaction, un catalyseur est consommé lors d’une étape puis régénéré lors d’une
étape ultérieure : il n’est pas consommé par la réaction (on le constate au document 2 où H+ est
consommé à l’étape (1) puis régénéré à l’étape (5)).
De plus, un catalyseur est sélectif : son action est spécifique à une réaction donné.
1.4. (1)
Groupe caractéristique : amino
Famille : amine
Groupe caractéristique : ester
Famille : ester

2. Vérification de la pureté du réactif
2.1.1. (0,5) On souhaite déterminer la pureté de l’acide 4-aminobenzoïque NH2-C6H4-COOH
mais celui-ci peut exister sous plusieurs formes en fonctions du pH comme le montre le
diagramme de prédominance suivant :
Initialement, la solution S a un pH égal à 3,8, comme pKa1 < pH < pKa2 donc c’est bien la forme
NH3+-C6H4-COO–(aq) qui prédomine et c’est donc sous cette forme que l’acide 4-aminobenzoïque
est titrée.
Rq : cette forme est un amphion (ou zwitterion) qui provient d’une autoprotonation de la molécule
NH2-C6H4-COOH qui possède un groupe acide COOH et une groupe base NH2.
2.1.2. (0,5) À la fin du titrage, le pH est proche de 12,5 ; l’espèce chimique dosée se trouve donc
sous sa forme d’anion NH2-C6H4-COO– (cf 2.1.1.).
pKa1 pKa2
pH
2,5 4,9
NH3+-C6H4-COO– NH3+-C6H4-COOH NH2-C6H4-COO–