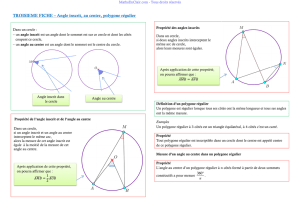
Angles inscrits, angle au centre, polygones réguliers 1 BDA BCA

Fiche Troisième - Angles inscrits, angle au centre, polygones réguliers
Arcs de cercle
Soit (C) un cercle de centre 0, A et B deux points distincts non diamétralement opposés
sur ce cercle. Il existe deux arcs de cercle ayant pour extrémités A et B : le petit arc noté
AB , et le grand arc :
Définitions : angle inscrit, angle au centre
Pour un cercle,
-un angle au centre est un angle ayant pour sommet le centre de ce cercle,
-un angle inscrit est un angle dont le sommet est un pont de ce cercle et dont les côtés
coupent le cercle.
L'arc intercepté par un angle au centre ou par un angle inscrit est l'arc de cercle compris
entre les deux côtés de l'angle.
BDA est un angle inscrit qui intercepte
le petit arc de cercle d'extrémités A et B.
BCA est un angle inscrit qui intercepte
le petit arc de cercle d'extrémités A et B.
BOA est un angle au centre qui
intercepte le petit arc de cercle
d'extrémités A et B.
Les deux propriétés
Propriété de l'angle inscrit et de l'angle au centre
Si, dans un cercle, un angle inscrit et un angle au centre interceptent le même arc,
alors la mesure de l'angle inscrit est égale à la moitié de la mesure de l'angle au centre.
Propriété des angles inscrits
Si, dans un cercle, deux angles inscrits interceptent le même arc,
alors ils ont la même mesure.
En utilisant la figure précédente, on a donc :
1
BDA BCA BOA
2
  .
Polygones réguliers
Un polygone régulier est un polygone dont tous les côtés ont la même longueur et dont
tous les angles ont la même mesure.
Exemples
Un polygone régulier à trois côtés est un triangle équilatéral, à quatre côtés c'est un carré.
Un polygone régulier à six côtés, appelé hexagone, est :
Centre d'un polygone régulier
Tout polygone régulier peut être inscrit dans un cercle dont le centre est appelé centre du
polygone régulier.
Propriété
Dans un polygone régulier , tous les angles au centre pour deux sommets consécutifs ont
la même mesure : 360°
nombredesommets .
Autrement dit : dans un polygone à ncôtés, de centre O et dont A et B sont deux
sommets consécutifs, on a :
360
AOB
n
.
[ MathsEnClair.com - Thiaude P - Tous droits réservés ]