Chapitre : Utiliser les nombres rationnels

Chapitre : Utiliser les nombres rationnels
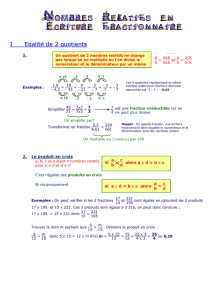
1 Nombre rationnels positifs ou negatif
Propriété
Un nombre rationnel peut s’écrire sous la forme 
bou − babec et bnombres entiers
positifs, b6=0.
Exemples
•−2
−3=2 3•−7
9=−7 9•5 −4=−5 4
Propriété
Un quotient ne change pas lorsqu’on multiplie ou divise son numérateur et son dénomi-
nateur par un même nombre non nul.
Exemples
0,3
−4=
0,3×10
−4×10 =−3 40 et −25 35 =−25÷5 35÷5=−5 7
2 Comparaison
Propriété
•Un nombre negatif est plus petit qu’un nombre positif.
•De deux nombres positifs, le plus petit est celui qui a la plus petite distance à zéro.
•De deux nombres négatifs, le plus petit est celui qui a la plus grande distance à zéro.
Remarque
Pour comparer deux quotients de dénominateurs différents, on les écrit d’abord avec le même
dénominateur.
Exemples
• − 3
4<10 3•2
7<5 7• − 7
5<−4 5
3 Addition, soustraction
Propriété : addition
Pour additionner deux nombres en écriture fractionnaire de même dénominateur, on ad-
ditionne les deux numérateurs et on garde le dénominateur commun.
Si ,bet csont des nombres relatifs avec cnon nul, alors : 
c
+
b
c
=
+b
c
Propriété : soustraction
Pour soustraire deux nombres en écriture fractionnaire de même dénominateur, on sous-
trait les deux numérateurs et on garde le dénominateur commun.
Si ,bet csont des nombres relatifs avec cnon nul, alors : 
c−b c
=
−b
c
4ième Cours Page 1/2

Exemples
11
3+
5
3=
11 +5
3=
16
3et 11 3−7 3=
11 −7
3=
4
3
Remarque
Si les dénominateurs sont distincts, avant d’additionner ou de soustraire, il faut transformer les
écritures fractionnaires de façon à les mettre au même dénominateur.
Exemples
5
2+
3
4=
5×2
2×2+
3
4=
10
4+
3
4=
13
4et 2 5−1 4=
2×4
5×4−1×5 4×5=
8
20 −5 20 =
7
20
4ième Cours Page 2/2