Les nombres complexes

Les
Les nombres nombres complexes complexes
Objectifs :
Savoir manipuler des nombres complexes
Savoir utiliser les formes algébrique et
trigonométrique et passer de l’une à l’autre
Calculer les racines nième d’un complexe
Résoudre des équations du second ordre à
coefficients complexes

Introduction
• XIVème siècle : invention des nombres
complexes représentant des racines
carrées de réels négatifs.
• Ces nombres ont permis de résoudre
toutes les équations du 2
nd
et 3
ième
degré
• Idée :i un nombre tel que i
2
=-1
Alors x
2
=-4 a pour solution 2i ou -2i

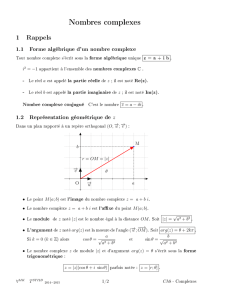
I-Définition et opérations dans C
• Définition: Un nombre complexe z peut se présenter comme une
somme z=a+bi
où a et b sont deux nombres réels, aest appelé partie réelle
b partie imaginaire
et i un nombre particulier tel que i2=-1
L’ensemble des nombres complexes se note C
Notation:
z=a+bi est appelé la forme algébrique de z
si a est un réel, c’est aussi un complexe a=a+0i, noté a
si b est un réel, le complexe 0+bi, noté bi, est appelé imaginaire pur
a) Définition

b) Opérations dans C
Soient z=a+bi et z’=a’+b’i
• Addition
z+z’=a+a’+ (b+b’)i
• Multiplication
zz’= (a+bi)(a’+b’i)=aa’-bb’+ (ab’+a’b)i
Remarque:
i=0+1xi et i
2
=-1+0xi=-1

Conclusion:
les calculs sur les nombres complexes
sous forme algébrique s’effectuent en
utilisant les mêmes règles de calcul
que celles des réels et en remplaçant i
2
par -1