Chapitre_2_fonctions_continues_et_reciproques

- 1 - Chapitre 2 : BTS 2 électrotechnique
Chapitre 2
Fonctions d’une variable réelle
I Fonction continue sur un intervalle de IR
A] Définition
Définition :
 Une fonction f est dite continue en x0 SSI f est définie au voisinage de x0 et
lim;x  x0 f(x) = f(x0).
 On dit que f est continue à droite en x0 si lim;x  x0+ f(x) = f(x0).
 On dit que f est continue à gauche en x0 si lim;x  x0 – f(x) = f(x0).
 On dit que f est continue en x0 SSI lim;x  x0+ f(x) = lim;x  x0 – f(x) = f(x0).
 On dit que f est continue sur I SSI elle est continue en tout point de I.
Interprétation graphique :
Cela signifie que l’on peut aller d’un point à un autre de la courbe Cf sans lever le crayon.
Exemples :
* La fonction inverse est continue sur IR+*, mais pas sur IR*.
* La fonction d’Heaviside n’est pas continue en 0, mais seulement à droite en 0 ; sur le
reste de IR elle est continue.
B] Continuité et dérivabilité
1) Rappels
Définition :
On dit que f est dérivable en x0 et de dérivée f ‘(x0) si on a :
f ‘ (x0) = lim;x
x0
Error!
=
Error!
Error!
.
Interprétation graphique :
La tangente à la courbe Cf au point d’abscisse x0 a pour coefficient directeur en f ‘(x0).
Faire un graphique.
2) Propriété
Théorème :
Toute fonction dérivable en x0 est continue en x0.
Démonstration :
ADMIS
Remarque :
La réciproque est fausse ; il existe des fonctions continues qui ne sont pas dérivables. ( Cf la
fonction valeur absolue ).
Exemples :
Les fonctions avec des points anguleux et les fonctions a tangente verticale ( cf la fonction racine
carrée en 0).
Exercices 11, 12, 14 et 16p42.
Exercice 17p43.

- 2 - Chapitre 2 : BTS 2 électrotechnique
Exercice 26p45.
3) Différentielle d’une fonction
Définition :
Soit f une fonction dérivable sur un intervalle I de IR contenant x0 ; on appelle différentielle de la
fonction f en x0, la fonction linéaire : h
Error!
f ‘(x0)h.
On note df(x0)(h) = f ‘ (x0) h ou df = f ‘(x0)dx.
Exemple :
Soit f(x) = x3 + x + 2. Ainsi f ‘(x) = 3x2 + 1. Donc df = ( ) 3x2 + 1 dx.
Ainsi en x0 = 2, on a df = 13 dx.
Propriété :
Les propriétés de la dérivée donnent des propriétés analogues pour la différentielle.
Ainsi on a :
 d( ) f+g = df + dg.
 d( ) fg = gdf + fdg.
 d
Error!
=
Error!
.
4) Image d’un intervalle par une fonction continue
Théorème :
L’image d’un intervalle I de IR par une fonction f continue est un intervalle J. I et J ne sont pas
forcément de même nature, mais si I est fermé, alors J est aussi fermé.
On peut aussi formuler cela de la manière suivante :
Pour tout k J, il existe au moins un x tel que f(x) = k.
Démonstration :
ADMIS
Faire une figure.
Théorème : Théorème de la bijection
Si f est une fonction continue strictement monotone sur un intervalle I de IR, alors f réalise une
bijection de I sur J = f(I).
On peut aussi formuler cela de la manière suivante :
Pour tout k J, il existe un unique x I tel que f(x) = k.
Démonstration :
ADMIS
Faire une figure.
II Fonction réciproque
A] Définition
Définition :
Si f est une bijection de I sur J, alors il existe une unique fonction notée f –1 tel f
Error!
f –1 = idJ et
f –1
Error!
f=idI. La fonction f–1 est appelée fonction réciproque de f.
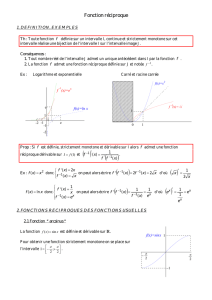
Exemples :
* la fonction carrée sur IR+ et la fonction racine carrée sur IR+.
* La fonction logarithme sur IR+* et la fonction exponentielle sur IR.

- 3 - Chapitre 2 : BTS 2 électrotechnique
Exercices 18 et 19p43.
B] Propriétés
Propriété :
Les fonctions f et f –1 ont les mêmes variations.
Représentation graphique :
Dans un repère orthonormal les courbes Cf et Cf–1 sont symétrique par rapport à la première
bissectrice d’équation y = x.
C] FONCTIONS RECIPROQUES DES FONCTIONS CIRCULAIRES
1) Fonction  arcsinus 
La fonction
f x x( ) sin
est définie et dérivable sur IR.
Pour obtenir une fonction strictement monotone on se place sur
l’intervalle
I  
2 2
;
.
Ainsi sur cet intervalle f réalise une bijection de
Error!
sur
Error!
.
Propriété :
La fonction
g x x( ) arcsin
est dérivable sur l’intervalle ]1; 1 [
de dérivée
arcsin'( )xx
1
12
.
Démonstration :
ADMIS
Propriété :
La fonction arcsin est strictement croissante sur [  1; 1 ].
Exercice 32p47.
0 1
1
f(x)=x2
f (x)= x
-1
1
e
-1
-2
1
e
1
e
-1
-2
f (x)=e
-1 x
f(x)=ln x
f(x)=sinx 
2
2
Définition :
La fonction réciproque de la fonction sinus est la fonction arcsinus définie sur l’intervalle
[  1; 1 ] par : sin y = x SSI y = arcsin x.
g(x)=arcsin x
2
2

- 4 - Chapitre 2 : BTS 2 électrotechnique
2) Fonction  arccosinus 
La fonction g(x) = cos x est définie et dérivable sur IR.
Pour obtenir une fonction strictement monotone on se place sur
l’intervalle
I0;
.
La fonction g réalise alors une bijection de
Error!
sur [  1; 1 ].
Propriété :
La fonction
g x x( ) arccos
est dérivable sur
l’intervalle ]1; 1 [
et de dérivée
2
1
1
)(arccos' x x
.
Démonstration :
ADMIS
Propriété :
La fonction arcos est strictement décroissante de
Error!
sur
Error!
.
Propriété :
Pour tout x
Error!
, on a arcsin x + arccos x =
Error!
.
Démonstration :
Posons f(x) = arcsin x + arccos x qui est définie et dérivable sur] –1 ; 1 [ ; comme somme de deux
fonctions définies et dérivables sur] –1 ; 1 [. Or f ‘ (x) =
Error!
–
Error!
= 0. Donc f est une
fonction constante sur ] –1 ; 1 [. Or f(0) = arccos 0 + arcsin 0 =
Error!
+ 0 =
Error!
.
Ainsi on conclut que f(x) = arcsin x + arccos x =
Error!
.
f(x)=cos x
2
Définition :
La fonction réciproque de la fonction cosinus est la fonction arccosinus définie sur l’intervalle
[  1; 1 ] par :
yxxy cosarccos 
g(x)=arccos x
2

- 5 - Chapitre 2 : BTS 2 électrotechnique
3) Fonction  arctangente 
La fonction h(x) = tan x est définie et dérivable
sur IR / {
2 k k; Z
}.
Pour obtenir une fonction strictement monotone on
se place sur l’intervalle
I  
2 2
;
.
Propriété :
La fonction h(x) = arctan x est dérivable sur IR de dérivée ( ) arctan ‘ x =
Error!
.
Propriété :
La fonction arctan est strictement croissante de IR sur
Error!
.
Exercice 30p47.
III Fonction d’une variable réelle à valeurs complexes
A] Définition
2
f(x)=tan x
2
Définition :
La fonction réciproque de la fonction tangente est la fonction arctangente définie sur IR par :
yxxy tanarctan 
2
g(x)=arctan x
2