Chapitre 11

B
A C
B
A C
E
D F
Chapitre 11 : TRIGONOMETRIE
A – Sinus, cosinus et tangente d'un angle aigu
a) Côtés d’un triangle rectangle
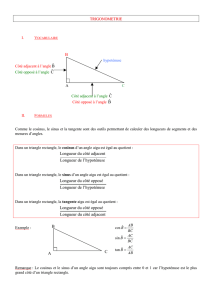
[BC] s'appelle l'hypoténuse
Pour l'angle
̂
B
,
[BA] est le côté adjacent et
|AC] est le côté opposé
Pour l'angle
̂
C
,
[CA] est le côté adjacent et
[AB] est le côté opposé
b) Définitions
Cosinus
̂
F
=
Côté adjacent
Hypoténuse
=
FD
FE
Sinus
̂
F
=
Côté opposé
Hypoténuse
=
ED
FE
Tangente
̂
F
=
Côté opposé
côté adjacent
=
ED
FD
On note en général cos
̂
F
sin
̂
F
et tan
̂
F
Repère 1 --------------------------------------------------------------------------------------------- Repère 1

B- APPLICATIONS
I. On connaît l’hypoténuse et un angle aigu :
on peut retrouver un des petits côtés.
47° 5 cm
On considère le triangle RST rectangle en R tel que ST = 5 cm et
̂
RST
= 47°.
1°) Calcul de RS
(côté adjacent -> utilisat° du cosinus)
Dans le triangle RST rectangle en R , on
a : cos
RST
=
RS
ST
Donc cos 47° =
RS
5
d’où SR = 5 × cos 47°
La calculatrice donne SR » 3,4 cm
2°) Calcul de RT
( côté opposé -> utilisation du sinus)
Dans le triangle RST rectangle en R , on
a : sin
RST
=
RT
ST
Donc sin 47° =
RT
5
d’où RT = 5 × sin 47°
La calculatrice donne RT » 3,7 cm
II. Calculer l’hypoténuse en utilisant le cosinus ou le sinus
On donne le triangle AFL ci-contre rectangle en L tel que
AL = 3cm et
AFL
= 34°. Déterminer FA à 1 mm près.
34°
Réponse :
Dans le triangle AFL rectangle en L , on a : sin
AFL
=
AL
AF
sin 34° =
3
FA
On obtient : AF =
3
sin 34 °
La calculatrice donne AF » 5,3 cm
Remarque :On pourrait retrouver de la même façon FA si on connaissait la longueur FL (côté
adjacent) en utilisant le cosinus
A
LF
R
S T

B
A
C
E
D F
III. Utilisation de la TANGENTE (retrouver un des petits côtés)
On considère un triangle EFG rectangle en E
tel que EF = 4 cm et
GFE
= 55°. 55°
Calculer EG à 1 mm près. 4 cm
Réponse :
Dans le triangle EFG rectangle en E , on a :
tan
GFE
=
EG
EF
tan 55° =
EG
4
d’où EG = 4 × tan 55°
Donc EG ≈ 5,7 cm
IV- Calcul d'un angle
Calculer la mesure de l'angle
̂
ABC
.
5
3 Dans le triangle ABC rectangle en A :
Cos
̂
ABC
=
AB
BC
Cos
̂
ABC
=
3
5
donc
̂
ABC
= arccos (
3
5
)
̂
ABC
≈ 53°
Calculer la mesure de l'angle
̂
EFD
.
5
4 Dans le triangle EDF rectangle en D :
sin
̂
EFD
=
ED
EF
sin
̂
EFD
=
4
5
donc
̂
EFD
= arcsin (
4
5
)
̂
EFD
≈ 53°
F
E G

G
I
H
Calculer la mesure de l'angle
̂
IGH
.
Dans le triangle GHI rectangle en I :
5 tan
̂
IGH
=
HI
GI
6 tan
̂
IGH
=
6
5
donc
̂
IGH
= arctan (
6
5
)
̂
IGH
≈ 50°