Analyse 4

Applications dérivables Théorème des Accroissements Finis FORMULES DE TAYLOR
Derivées
Brahim Boussouis
Département de Mathématiques, Faculté des Sciences de Fès.
Octobre 2013
Brahim Boussouis Derivées

Applications dérivables Théorème des Accroissements Finis FORMULES DE TAYLOR Applications diffèrentiables Régles de dérivation Extrema relatifs
Sommaire
1Applications dérivables
Dérivées d’un côté
Interprétation géométrique de la dérivée
Applications diffèrentiables
Dérivées d’ordre supérieur
Régles de dérivation
Extrema relatifs
2Théorème des Accroissements Finis
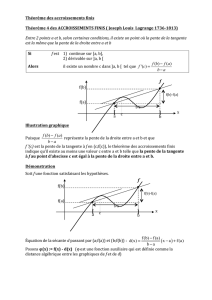
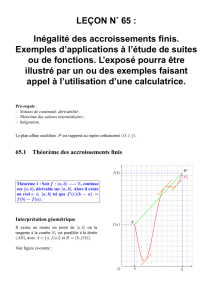
Théorèmes de Rolle et des accroissements finis
Applications du théorème des accroissements finis
Dérivées et monotonie
Règle de l’Hôpital
3FORMULES DE TAYLOR
Formule de Taylor-Young
Allure d’une fonction au voisinage d’un point
Application aux extremums
Formule de Taylor-Lagrange
Brahim Boussouis Derivées

Applications dérivables Théorème des Accroissements Finis FORMULES DE TAYLOR Applications diffèrentiables Régles de dérivation Extrema relatifs
Définition
Soient Iun intervalle de Rnon réduit à un point , x0∈Iet f:I→R. On dit
que fest dérivable en x0si la limte
lim
x→x0
f(x) − f(x0)
x−x0
=lim
h→0
f(x0+h) − f(x0)
h,(x=x0+h)
existe (dans R). Cette limite (qui est alors unique) est appelée dérivée de f
au point x0, et notée par :
f0(x0),Df (x0),df
dx (x0)ou dy dx x=x0
si y=f(x).
On dit que fest dérivable sur I, si fest dérivable en tout point de I. La
fonction f0:x∈I7−→f0(x)∈Rs’appelle la fonction dérivée de f.
Brahim Boussouis Derivées

Applications dérivables Théorème des Accroissements Finis FORMULES DE TAYLOR Applications diffèrentiables Régles de dérivation Extrema relatifs
Exemples
ISi f est constante sur I, alors f est dérivable sur I et f 0≡0.
If(x) = xn, n ∈N∗: Pour tout x0∈R,ona:
lim
h→0
f(x0+h) − f(x0)
h=lim
h→0
(x0+h)n−xn
0
h
=lim
h→0
C1
nhxn−1
0+C2
nh2xn−2
0+·· · +Cn
nhn
h
=C1
nxn−1
0=nxn−1 0.
Donc f est dérivable en x0et f 0(x0) = nxn−1
0.
If(x) = sin x : Pour tout x0∈R,ona:
lim
h→0
f(x0+h) − f(x0)
h=lim
h→0
2 sin h
2cos(x0+h 2)
h
=cos x0.
Donc f est dérivable en x0et f 0(x0) = cos x0.
Brahim Boussouis Derivées

Applications dérivables Théorème des Accroissements Finis FORMULES DE TAYLOR Applications diffèrentiables Régles de dérivation Extrema relatifs
Théorème et définition
Si x06=sup I (resp. x06=inf I) et si le taux d’accroissement f(x)−f(x0)
x−x0admet
une limite à droite (resp. à gauche) en x0, on dit que f est dérivable à droite
(resp. à gauche ) en x0. Cette limite est appelée dérivée à droite (resp. à
gauche) de f en x0, et notée par f 0
d(x0)(resp. f 0
g(x0)).
Pour que f soit dérivable en un point x0∈]inf I,sup I[, il faut et il suffit qu’elle
soit dérivable à droite et à gauche en x0et que f 0
d(x0) = f0
g(x0).
Par exemple, la fonction f(x) = |x|n’est pas dérivable en 0, car
f0
d(0) = 16=f0
g(0) = −1.
Proposition
Si f est dérivable à droite ( resp. à gauche ) en x0, alors f est continue à
droite ( resp. à gauche ) en x0. En particulier si f est dérivable en x0, alors f
est continue en x0.
Par exemple, si fest dérivable à droite en x0, alors
lim
x→x+
0
[f(x) − f(x0)]=lim
x→x+
0
(x−x0)f(x) − f(x0)
x−x0
=0×f0
d(x0) = 0.
Remarque
La réciproque est fausse : la fonction f (x) = xsin 1
xsi x 6=0
0si x =0est continue
en 0sans être dérivable en ce point. De même, la fonction x 7→|x|est
continue en 0sans y être dérivable.
Brahim Boussouis Derivées