cours - Stepec Muriel

Chapitre 3 Terminale S
Stepec Page 1 sur 5 769907679
DERIVATION
I Définitions (rappels chap 4 1ière )
1) Définition: Soit f une fonction définie sur Df et a un réel élément de Df.
On dit que f est dérivable en a lorsque le taux d'accroissement de f en a admet une limite
finie l en a .
lim;h  0
Error!
= l ou écrit autrement:
Error!
Error!
= l
Dans ce cas, l est appelé le nombre dérivé de f en a et on le note f '(a).
2) Tangente
Si f est dérivable en a, la courbe Cf admet au point A ( a ; f ( a ) ) une tangente Tg de coefficient
directeur f'(a). Une équation de la tangente en ce point est : y = f’(a )(x – a) + f(a)
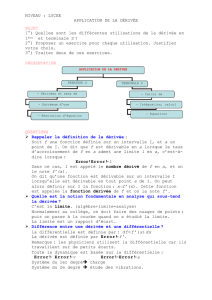
3) Approximation affine locale
A proximité du point A la courbe et sa tangente sont très
proches, localement on peut remplacer la fonction f par la
tangente Tg .
L'approximation affine de f pour x voisin de a est:
f(x)  f '(a) (x-a) + f(a)
L'approximation affine locale de f(a +h) pour h voisin de 0 est:
f(a +h)  f '(a) h + f(a)
II Fonctions dérivées (rappels chap 4 1ière )
1) fonctions dérivées de fonctions de références
2) Opérations sur les fonctions dérivables
Soit u et v deux fonctions dérivables sur un intervalle I alors:
Fonction
Ensemble de définition
Dérivée
Ensemble de dérivabilité
f(x) = k
IR
f '(x) = 0
IR
f(x) = ax + b
IR
f '(x) = a
IR
f(x) = x2
IR
f'(x) = 2x
IR
f(x) =
x
1
IR
*
f'(x) = -
2
1
x
IR
*
f(x) = x
[0 ; + ∞[
f'(x) = Error!
] 0 ; + ∞[
f(x) = xn et n  N*
IR
f'(x) = nxn-1 , n 
ZZ
IR
et n ≥ 1
f(x) = sin x
IR
f'(x) = cos x
IR
f(x) = cos x
IR
f'(x) = - sin x
IR
f(x) = tan x
IR
-{Error! +k}
f(x) = 1+tan2x = Error!
IR
-{Error! +k}
f ( a + h )
f ( a ) + h f ’ ( a )
f ( a )
M
M’
A
Error!
O Error! a a + h
Cf Tg
T semble proche de Cf
autour du point A

Chapitre 3 Terminale S
Stepec Page 2 sur 5 769907679
Fonction
Fonction dérivée
Exemple
u + v
u' + v'
Si f(x) = x + x alors f'(x)=
uv
u'v + uv'
Si f(x) = x3 x alors f'(x) =
ku où k est un réel
ku'
Si f(x) = 4cosx – Error! alors f'(x) =
un
nu'un-1
Si f(x) = (3cosx – 2)5 alors f'(x) =
Error!
-Error!
Si f(x) = Error!alors f'(x) =
Error!
Error!
Si f(x) = Error! alors f'(x) =
u (ax +b)
au'(ax + b)
Si f(x) = sin(2x -5) alors u(x) = et a =
Donc f'(x) =
Exercices : 3, 6, 10, 12, 14, 16 p 72
III Application de la dérivation (rappels chap 5 1ière )
1) Sens de variation
Théorème: Soit f une fonction dérivable sur un intervalle I:
Si la dérivée f ' est nulle sur I, alors f est constante sur I.
Si la dérivée f ' est strictement positive sur I, sauf peut-être en des points isolés où elle
s'annule, alors f est strictement croissante sur I.
Si la dérivée f ' est strictement négative sur I, sauf peut-être en des points isolés où elle
s'annule, alors f est strictement décroissante sur I.
exemple: Etudier les variations de f (x) = x3, puis g(x) = x3 – 6x2 + 4
2) Extremum local (revoir chap5 1ière )
Théorème: Soit f une fonction dérivable sur un intervalle ouvert I, et c un réel de I
1) Si f admet un extremum local en c alors f '(c) = 0
2) Si en c la dérivée f ' s'annule en changeant de signe, alors f admet un extremum local
en c.
Exemple: Donner les extremums locaux des fonctions f et g données précédemment.
Exercices : 22, 23, 25, 26 p 73

Chapitre 3 Terminale S
Stepec Page 3 sur 5 769907679
3) Etude de la fonction tangente f(x) = tan x
Domaine de définition :
Parité:
Périodicité:
Dérivée de tan x : Démontrer que tan x est dérivable sur Df et calculer sa dérivée
Etude de f'(x) sur [0;
Error!
[: (signes + limites)
Tableau de variation
x
0
Error!
tan'(x)
tan(x)
IV Dérivée d'une fonction composée
1) Théorème fondamental
Théorème: g est une fonction dérivable sur D' , u une fonction dérivable sur D , et pour tout x de D ,
u(x) est élément de D'. (autrement dit : u(D) D' )
Alors la fonction f définie par f(x) = g◦u (x) = g(u(x)) est dérivable sur D et
pour tout x de D on a :
f '(x) = g'(u(x)).u'(x))
ROC Démon:

Chapitre 3 Terminale S
Stepec Page 4 sur 5 769907679
2) Dérivation de u
Théorème: Soit u une fonction strictement positive et dérivable sur D.
Alors la fonction f définie par f(x) = u(x) est dérivable sur D et pour tout x de D on a :
f '(x) =
Error!
Démon.:
3) Dérivation de un
Théorème: Soit u une fonction dérivable sur D et n 
Error!
*
Si n > 0, la fonction f définie par f(x) = [u(x)]n est dérivable sur D et pour tout x de D on a :
f' (x) = n [u(x)]n-1 u '(x)
Si n<0 et si la fonction u ne s'annule pas sur D alors la fonction f définie par f(x) = [u(x)]n
est dérivable sur D et pour tout x de D on a :
f' (x) = n [u(x)]n-1 u '(x)
Démon.:
Exercices: 27, 29, 30, 32, 36 p 74
V Dérivées successives
Définition : f est une fonction dérivable sur Df .
La fonction dérivée f ' s'appelle également dérivée première ou d'ordre 1 de f

Chapitre 3 Terminale S
Stepec Page 5 sur 5 769907679
Si f ' est dérivable sur D , sa fonction dérivée notée f '' est appelée dérivée seconde ou
d'ordre 2.
Ainsi de suite pour n > 2 , on définit la fonction dérivée nième comme la fonction dérivée de
la dérivée (n-1) lorsqu'elle est dérivable.
Pour n > 1 on a f n = (f n-1) '
Remarque: Nous avions établit en 1ière la dérivée comme étant la vitesse instantanée de la même manière
on peut établir la dérivée seconde comme l'accélération instantanée.
Exercices : 38, 39, 40, 41, 42, 43 p 75 et 61p77 et 84p82