baccalaureat de l`enseignement general – madagascar

BACCALAUREAT DE L’ENSEIGNEMENT GENERAL – MADAGASCAR
Série : C - SESSION 2003
Epreuve de : Sciences Physiques
Durée : 4 heures
CHIMIE ORGANIQUE (3 points)
1. Un alcène de formule R – CH = CH – R’ est hydraté en présence de l’acide sulfurique. (Les
radicaux R et R’ sont des groupes alkyles).
a) Quels sont les composés A et B susceptibles d’être obtenus ?
b) Ces deux composés A et B sont chiraux ; représenter les deux énantiomères de
l’un d’eux.
2. On fait réagir 3,7 g de l’alcool obtenu par l’hydratation avec une solution de permanganate de
potassium (K+, MnO ) en milieu acide et on obtient un composé C de masse 3,6 g.
Ecrire l’équation traduisant la réaction redox et en déduire la formule brute de l’alcool.
3. Quelle conclusion peut-on en tirer quant aux composés A et B ?
On donne : H = 1 gmol– 1 ; C = 12 gmol– 1 ; 0 = 16 gmol– 1.
CHIMIE GENERALE ET MINERALE (3 points)
On considère les trois solutions aqueuses suivantes, à 25°C :
- S1 est une solution aqueuse d’hydroxyde de sodium de concentration
C1 = 5.10– 2 mol l– 1.
- S2 est une solution aqueuse d’acide méthanoïque de concentration C2 = 10– 1 mol l– 1.
- S3 est une solution aqueuse de méthanoate de sodium de concentration
C3 = 5.10– 2 mol l– 1.
1. Le pH de la solution S1 est égal à 12,7. Montrer que cette valeur est en accord avec la
concentration C1 de la solution S1.
2. A 40 cm3 de la solution S3, on ajoute 10 cm3 de S2. On obtient un mélange de
pH = 4,1.
a) Faire le bilan des espèces chimiques présentes dans le mélange à l’équilibre et calculer
leurs concentrations molaires.
b) En déduire le pkA du couple HCOOH / HCOO – .
3. A 40 cm3 de la solution S1, on ajoute progressivement la solution S2. Pour quelle valeur V du
volume de S2 versé le pH du mélange est égal à 3,7 ?
- On admet que : [OH –] << [H3O+] << [Na+] pour les questions 2 et 3.
- On donne log 2 0,3 et log 1,25 0,1.
ELECTROMAGNETISME (4 points)
Dans ce problème, on prendra
2 10.
Un dipôle (A,B) est constitué par l’association en série d’un conducteur ohmique de
résistance R, d’une bobine de résistance négligeable et d’inductance L, et d’un condensateur de
capacité C. On applique aux bornes de ce dipôle une tension :
tN2cos10tuAB 
V, fournie
par un générateur de tension sinusoïdale, de fréquence N réglable.
On fait varier la fréquence N de 100 à 1000 Hz et on mesure l’intensité maximale
m
du
courant traversant le dipôle à chaque valeur de N. On obtient le tableau suivant :
N (Hz)
100
200
300
400
500
600
700
800
900
1000
m
(mA)
5
12
23
45
63,5
45
32
24
19
16
1. a)Tracer sur le document 1b la courbe donnant la variation de l’intensité maximale
m
en
fonction de la fréquence N.
b) En déduire la fréquence de résonance N0 et l’intensité maximale I0 correspondante.

2. a)Calculer la résistance R du conducteur ohmique.
b) La bande passante est définie par les fréquences N1 et N2 (N1 < N2) pour lesquelles
2
I
NI 0
2m 
- Déterminer graphiquement les valeurs de N1 et N2.
- En déduire la largeur en fréquence N = N2 – N1 de la bande passante, ainsi que
la valeur du facteur de qualité
N
N
Q0
du circuit.
c) Calculer alors les valeurs de C et L.
N.B. : Pour simplifier le calcul de C et L, on prendra R 157  et on remarquera
2
1,57.
PHYSIQUE NUCLEAIRE (2 points)
Le nucléide du polonium
Po
210
84
est radioactif en donnant un noyau
Pb
206
82
. La demi-vie est
T = 140 jours.
1. Ecrire l’équation traduisant la désintégration du
Po
210
84
. De quel type de désintégration s’agit-il
2. A l’instant initial t = 0, un échantillon de matière a une activité radioactive
A0 = 1,25.1012 Bq, due à la présence de
Po
210
84
radioactif.
a) Calculer le nombre moyen
o
N
des noyaux radioactifs présents dans cet échantillon
à cet instant.
En déduire la masse m0 de
Po
210
84
correspondante.
b) Calculer l’activité radioactive de cet échantillon à t = 150 jours.
3. A quel instant, 75 % des noyaux initiaux sont-ils désintégrés ?
Données : - masse atomique molaire du
Po
210
84
: M = 210 g mol – 1.
- nombre d’Avogadro : N = 6.1023 mol – 1.
- ln 2 0,7 et e– 0,75 0,47.
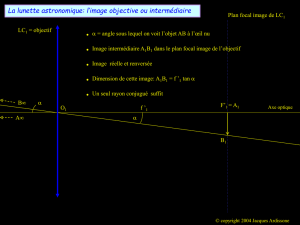
OPTIQUE GEOMETRIQUE (2 points)
1. On étudie l’image du mât d’un voilier, donnée par une lentille mince L1, de centre optique
O1, et de vergence C1 = 20 . Le mât AB, de hauteur 4,5 m, constitue un objet réel, situé à
50 m de L1. On suppose que le pied A du mât est situé sur l’axe optique horizontal de L1, et
que le mât est perpendiculaire à cet axe.
Donner, par calculs, les caractéristiques de l’image A1B1 du mât.
2. On place après la lentille L1, une autre lentille mince L2 de vergence C2 = – 50  et dont
le centre optique O2 est à 3,5 cm de O1. Les axes optiques des deux lentilles sont
confondus.
a) L’image A1B1 du mât à travers L1 devient un objet pour L2. Placer A1B1 sur le document 1a et
préciser s’il s’agit d’un objet réel ou virtuel pour L2.
b) On appelle A2 B2 l’image de A1B1 obtenue à travers L2.
- Construire sur le même document 1a cette image.
- Déterminer, par calculs, ses caractéristiques.
MECANIQUE (6 points)
Dans ce problème on prendra || || = 10 ms – 2. Tous les calculs seront effectués à 10– 2 près.
Un solide (S) de masse m = 50 g, de dimension négligeable, peut glisser sur une piste ABCD située
dans un plan vertical :

- AB est la ligne de plus grande pente d’un plan incliné d’un angle = 30° par
rapport à l’horizontale ; AB = 1,6 m.
- BCD est le quart d’un cercle de centre I et de rayon R 0,9 m ; C est situé sur la
verticale passant par I.
1. On néglige les frottements. (S) part du point A sans vitesse.
a) Calculer sa vitesse en B, en C et en D.
b) Calculer l’intensité de la force
N
exercée par la piste sur (S) en C et en D.
c) Donner les caractéristiques du vecteur vitesse
D
V
de (S) au point D.
2. On néglige la résistance de l’air. A partir du point D, (S) tombe dans le vide avec la vitesse
D
V
précédente. Le point C est situé à la hauteur h = 1,55 m du sol horizontal.
a) Donner l’équation cartésienne de la trajectoire du mouvement de (S) à partir du point
D, dans le repère (O ; x, z).
b) Jusqu’à quelle hauteur H au-dessus du sol horizontal monte le solide (S) ?
c) Calculer la distance OP où P est le point d’impact de (S) sur le sol horizontal.
3. Dans cette question, la piste exerce au mouvement de (S) une force de frottements
f
,
parallèle et de sens contraire à sa vitesse à chaque instant, et d’intensité constante le long
de ABCD. Partant de A sans vitesse, (S) s’arrête au point D.
a) Etablir en fonction de m, g, R et , l’expression algébrique du travail
f
W
de la force
de frottements entre les points A et D. Calculer
f
W
.
b) En déduire l’intensité de la force
f
.
On donne : cos 30° 0,86.
Echelles :
Sens positif de la propagation de la lumière