Il faut 20 œufs pour préparer une mousse au chocolat - E

5° contrôle de math du vendredi 18 décembre 2009
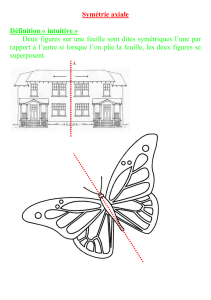
I. Compléter les définitions suivantes
– Le symétrique d’un point A par rapport à un point I est
– Le symétrique du cercle de centre A et de rayon r est
– Le symétrique d’un segment [AB] par rapport à un point O est
II. Répondre par vrai ou faux en donnant un contre-exemple si la phrase est fausse.
a) Deux droites parallèles sont symétriques par rapport à un point :
c) Deux segments de même longueur sont symétriques :
III. Tracer le symétrique du triangle ABC par rapport au point C.
Tracer en rouge le symétrique du triangle ABC par rapport au point M.
A
B
C
M
V. Sur la figure ci-dessous, on sait que A est le symétrique de B par rapport au point O, de
même que D est le symétrique de C par rapport à O. Le point O a été effacé.
En utilisant uniquement une règle non graduée et un compas, tracer le symétrique N de M
par rapport à O en laissant vos traits de construction.

VI. On trace trois cercles de rayons différents, mais ayant le même centre.
On dessine un triangle ABC tel que chacun de ses sommets soit situé sur l’un des cercles.
Construire le symétrique du triangle ABC par rapport à O en n’utilisant seulement qu’une
règle non graduée. Expliquer la construction.
III. Si on suppose qu’il y a proportionnalité entre le nombre d’œufs pour préparer une mousse
au chocolat et le nombre de personnes pour laquelle elle est prévue, remplir les trous
Il faut 20 œufs pour préparer une mousse au chocolat pour personnes.
Il faut 4 œufs pour préparer une mousse au chocolat pour 5 personnes.
Il faut œufs pour préparer une mousse au chocolat pour 120 personnes.
Calculer la mesure de l’angle rouge

5° correction du contrôle de math du vendredi 18 décembre 2009
I. Compléter les définitions suivantes
– Le symétrique d’un point A par rapport à un point I est le point A’ tel que I est le milieu du
segment [AA’].
– Le symétrique du cercle de centre A et de rayon r est le cercle de centre A’ (symétrique de A
par rapport à I) et de même rayon r.
– Le symétrique du segment [AB] par rapport à un point O est le segment [A’B’] tel que [AB] et
[A’B’] sont parallèles et de même longueur.
II. Répondre par vrai ou faux en donnant un contre-exemple si la phrase est fausse.
a) Deux droites parallèles sont symétriques par rapport à un point : vrai
On prend deux points A et A’ sur chacune des deux droites, on peut tracer le milieu M du
segment [AA’]. Il suffit de tracer une droite (BB’) passant par le point M.
c) Deux segments de même longueur sont symétriques : faux
Si on suppose que C est le symétrique de B par rapport à O, le symétrique de A est le point A’
et non le point D
Pour que deux segments soient symétriques par rapport à un point, il faut qu’ils soient
parallèles et de même longueur.
III. Tracer le symétrique du triangle ABC par rapport au point C.
Tracer en rouge le symétrique du triangle ABC par rapport au point M.
Exemple : pour construire le symétrique C’’ de C par rapport à M, il suffit de compter le
nombre de carreaux pour aller de C à M : 5 à Gauche et 1 en Haut et reporter ce chemin à
partir de M, ce qui donne le point C’’.

V. Deux points symétriques et le centre de symétrie sont alignés, donc le point O est à la fois
sur les droites (AB) et (CD), donc à leur intersection.
On trace la droite (OM), car N est sur la droite (OM), puis le cercle de centre O et de rayon
OM car O est le milieu de [MN] (définition du symétrique d’un point par rapport à un point) ;
il coupe la droite (OM) au point N qui est le symétrique de M par rapport à O.
Remarque : ACBD est un parallélogramme, car ses diagonales se coupent en leur milieu.
VI. On trace trois cercles de rayons différents, mais ayant le même centre.
On dessine un triangle ABC tel que chacun de ses sommets soit situé sur l’un des cercles.
Construire le symétrique du triangle ABC par rapport à O en n’utilisant seulement qu’une
règle non graduée. Expliquer la construction.
Deux points symétriques et leur centre de symétrie sont alignés. La symétrie centrale conserve
les longueurs.
Si on appelle A’ le symétrique de A par rapport à O, les points A, O, A’ sont alignés et OA = OA’
Donc A’ est sur le cercle de centre O et de rayon [OA] et [AA’] est un diamètre de ce cecle.
Pour construire A’, il suffit donc de tracer la droite (AO) ; A’ est donc le point d’intersection de
(OA) et du cercle. Puisque chacun des trois sommets du triangle ABC est situé sur un cercle
de centre O, donc leur symétrique se situe sur le même cercle et on fait deux fois la même
construction pour B et C. Il suffit ensuite de relier les poits A’, B’ et C’ (triangle rouge).

III. Il faut 20 œufs pour préparer une mousse au chocolat pour 25 personnes.
Il faut 4 œufs pour préparer une mousse au chocolat pour 5 personnes.
Il faut 96 œufs pour préparer une mousse au chocolat pour 120 personnes.
Une erreur à ne pas commettre était de considérer qu’il y avait 1 personne de plus que d’œufs.
Le coefficient multiplicateur permettant de passer de 4 à 5 est
4
5
, car 4 
4
5
= 5 ; donc puisqu’
il faut 4 œufs pour préparer une mousse au chocolat pour 5 personnes, avec 20 œufs, on peut
préparer une mousse au chocolat pour 25 personnes. (multiplication par 5)
Inversement, pour préparer une mousse au chocolat pour 5 personnes, il faut 4 œufs, donc
pour préparer une mousse au chocolat pour 120 personnes, il faut 96 œufs (multiplication
par 24) ou encore, il faut 96 œufs pour préparer une mousse au chocolat pour 120 personnes.
Calculer la mesure de l’angle rouge
AB = AC, donc ABC est un triangle isocèle en B ; les deux angles à la base (BAC) et (ACB) ont
même mesure. L’angle (ACB) mesure 82°, donc l’angle (CAB) mesure aussi 82°.
La somme des mesures des angles d’un triangle est égale à 180° ; dans le triangle ABC, on
connaît la mesure des angles (BAC) = 82° et (ACB) = 82°, on en déduit la mesure de l’angle
(ABC) : 180  82  82 = 16°
(ABD) est un angle droit et les angles (ABC) et (CBD) sont complémentaires.
(ABD) = (ABC) + (CBD) donc (CBD) = (ABD)  (ABC) = 90  16 = 74°