Proposition de progression – Stage LX et CEC 30 janvier 2017

Proposition de progression – Stage LX et CEC 30 janvier 2017
Avant-propos
 Ressources recommandées : « 1,2,3, Codez », ed. Le Pommier (téléchargeable gratuitement sur le
site lamap)
GeoGebra
Scratch
 En CM : on est à 95% sur la géométrie dessinée, l’abstraction est développée à partir de la 6°
 Lier géométrie plane/ dans l’espace. Partir de l’environnement de l’élève, d’un objet du quotidien
et le modéliser pour en extraire l’étude des figures planes.
ESPACE ET GEOMETRIE
CYCLE 3
Début d’apprentissage
(Attendus fin CM1)
Milieu
(Attendus fin CM2)
Fin d’apprentissage
(Attendus fin 6°)
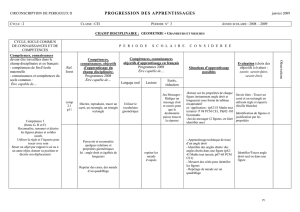
Se repérer et se déplacer dans l’espace en utilisant ou en élaborant des
représentations
Se repérer sur un quadrillage à l’aide de
coordonnées (sans ordre) : (D,4) ou
(4,D)
Se repérer sur un plan, une carte à
l’aide de coordonnées (sans ordre) :
(D,4) ou (4,D)
Se repérer sur un quadrillage à
l’aide de coordonnées =
(abscisses, ordonnées).
Se déplacer suivant les 4 directions (N,
S, E, O) ou (→, ←, ↑, ↓) sur un plan ou
une carte.
Se déplacer réellement (ex CO) :
situer sa position sur une carte, se
déplacer selon des instructions
données (avancer, faire un quart de
tour à droite ou gauche).
Se repérer sur une carte (avec les
échelles) et se déplacer (en
utilisant les angles.
Rechercher l’itinéraire le plus
court et le confronter à la réalité
(passage 2D à 3D).
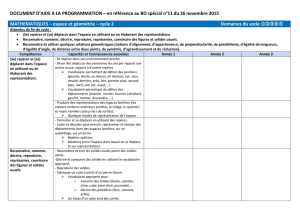
Reconnaitre, nommer, décrire, reproduire, représenter, construire, quelques
solides et figures géométriques
Reconnaitre, nommer et décrire des
solides simples : le cube, le pavé, la
pyramide à base carrée, la boule, le
cône
Décrire
Reconnaitre les patrons des
différents solides parmi des patrons
et le vérifier.
Construire les patrons du cube.
Construire le patron du pavé droit.
Reconnaitre les patrons des
différents solides.
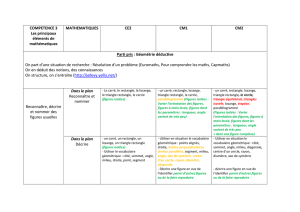
Reconnaitre, nommer, reproduire et construire des figures simples (carré, rectangle ≠losange, cercle, triangle) par les
côtés et les angles de manière perceptive et avec une validation instrumentée (équerre, règle, compas)
Classer les figures planes
(exemples : un carré est un
rectangle particulier ; un carré est
un losange particulier …)
Carré, rectangle, losange
A partir des propriétés concernant les côtés et les angles des figures
Carré, rectangle, losange
A partir des propriétés concernant
les diagonales des figures
Cercle
A partir des composantes essentielles : cercle et rayon (en tant qu’écart de
Cercle
A partir de la définition : à égale

Proposition de progression – Stage LX et CEC 30 janvier 2017
compas)
distance d’un point.
Triangles
Reconnaitre, décrire et nommer les 3
types : rectangle (lié à l’équerre) ;
isocèle et équilatéral (lié à la mesure)
Construire le triangle rectangle avec
équerre et avec mesure donnée.
Construire les triangles isocèle et
équilatéral avec compas (sans
formaliser) avec une mesure donnée.
Triangles
Construire les 3 types : rectangle
(lié à l’équerre et à la définition du
cercle et au rapporteur) ; isocèle
et équilatéral (lié à la mesure et à
la définition du cercle et au
rapporteur) avec mesures
données.
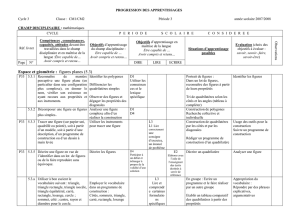
Programmes de construction
Lire et exécuter un programme à 2
figures au moins.
Rédiger un programme de
construction à partir d’une figure
complexe donnée avec une aide
majeure : exemples
=> Donner les programmes dans le
désordre
=> Donner le début du programme
=> Donner les mots clés à utiliser
(lexique de géométrie)
Rédiger un programme de
construction à partir d’une figure
complexe donnée avec ou sans
aide mineure :
Exemples
=> Donner les mots clés à utiliser
(lexique de géométrie)
Réaliser une figure simple ou une figure composée de figures simples à l’aide d’un logiciel.
Prise en main du logiciel
Construire des figures simples sans
passer par les propriétés
géométriques. Exemple : découverte
des fonctionnalités : point, segment,
droite, parallèles, perpendiculaires,
polygones, symétrie axiale.
Construire des figures simples en
passant par les propriétés
Rédaction d’un programme de
construction.
Reconnaitre et utiliser quelques relations géométriques
Alignement.
Identification de droites
perpendiculaires (gabarit, équerre) et
construction (droite perpendiculaire
passant par un point sur la droite ou le
plan).
Reconnaissance de droites parallèles
(en s’appuyant sur les propriétés du
rectangle).
Construction de droites parallèles (à
l’aide de l’équerre).
Construction des droites parallèles et
perpendiculaires au compas.
Distance entre deux points
Distance entre un point et une droite.
Reste à faire symétrie axiale