U [kV]

3
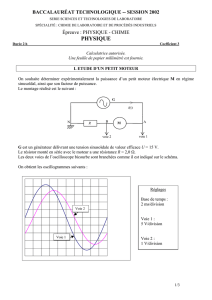
1. TERMINOLOGIE ET METHODE
La méthode des plans d’expériences est un outil permettant au chercheur, au concepteur,
mais aussi à l’ingénieur de production de mesurer l’importance de chacun des paramètres d’un
processus ou d’un produit, et de déterminer leurs valeurs les plus favorables. Cette méthode est
intéressante de mettre en œuvre dans les situations où les paramètres en question sont
nombreux et leurs effets difficilement modélisables par des lois classiques de la physique.
L’acquisition des connaissances sur le comportement d’un système par rapport aux
facteurs susceptibles le modifier s’appuie sur des expériences permettant de mesurer une ou
plusieurs réponses. A partir des résultats des mesures, il est possible d’établir les effets des
différents facteurs sur les réponses, ainsi que leurs interactions. La méthode des plans
d’expériences permet d’évaluer ces effets et interactions, en minimisant le nombre
d’expériences tout en maximisant la précision du résultat.
Les concepts et la méthodologie des plans d’expériences seront introduits en s’appuyant
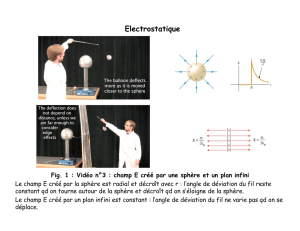
sur l’exemple concret du processus de séparation électrostatique.
1.1. Le processus de séparation électrostatique des matériaux granulaires
La séparation électrostatique des matériaux granulaires est produite par les forces
électriques agissant sur les granules qui ont des caractéristiques physiques différentes, qui
sont chargés ou polarisés, et qui se trouvent dans un champ électrique intense.
Dans les installations utilisées pour la séparation électrostatique des matériaux isolants
et métalliques provenant des déchets de câbles électriques, par exemple (Fig. 1.1), le champ
électrique intense est produit entre une ou plusieurs électrodes à potentiel électrique élevé
(plusieurs dizaines de milliers de volts) et une électrode cylindrique tournante liée à la terre.
Fig. 1.1. Séparateur électrostatique industriel ;
1 : électrode cylindrique tournante reliée à la terre ; 2 : transporteur à goulotte oscillante;
3 : électrode ionisante ; 4 : électrode électrostatique ; 5 : palette.
3
4
1
2
&
&
5

4
1.1.1. Rappel des grandeurs fondamentales de l’électrostatique
a) Charge électrique. Celle-ci est une propriété fondamentale de la matière qui respecte le
principe de conservation. Elle peut prendre deux formes, que l'expérience amène à considérer
comme « opposées »; on les qualifie arbitrairement de positive et négative. Deux charges de
même nature, deux charges positives par exemple, se repoussent, alors que deux charges de
nature opposée s'attirent.
La charge électrique peut être directement mesurée avec un électromètre. Son unité est le
coulomb (1 C). Les particules observées possèdent des charges qui sont des multiples entiers de
la charge élémentaire qui est une constante physique fondamentale.
Les charges électriques interviennent dans de nombreux phénomènes. Le premier
phénomène qui nous intéresse est la force F d'attraction ou de répulsion qui existe entre deux
corps ayant les charges Q1 et Q2, située à une distance d l’un par rapport à l’autre. La loi de
Coulomb exprime cette force électrique :
F = (Q1Q2) / (4  0 d2) (1.1)
où 0 =1 / (4  0 . 9.10 9) F / m est une constante (la permittivité électrique du vide). Si les
charges sont de la même polarité, la force (positive) est une force de répulsion. Si les charges
sont de polarités contraires (Q1 = qA < 0 et Q2 = qB > 0), la force (négative) est une force
d'attraction (Fig. 1.2).
Fig. 1.2. Force d’attraction (interaction coulombienne) entre deux particules chargées
de polarités opposées.
b) Champ électrique. Dans les installations électriques, comme les séparateurs
électrostatiques, il y a généralement plusieurs corps chargés ayant des configurations
complexes. Dans ce cas, le calcul de la force électrique à l'aide de la loi de Coulomb devient
long. Pour s’affranchir de ce problème, il convient de calculer le champ électrique E produit
par une charge Q1 dans un point P située à une distance rP de celui-ci :
E = k Q1 / rP 2 (1.2)
En ce point, le vecteur champ électrique est dans la même direction que le vecteur force
électrique F exercé sur une charge positive Q2 placée en ce point :
F = Q2E (1.3)
Une particule chargée dans un champ électrique possède une accélération proportionnelle
à la force électrique exercée sur elle (en supposant que la force électrique est seule). Le vecteur
accélération de la particule se trouve dans la direction du vecteur force électrique. Cette
propriété nous permettra de calculer ensuite les trajectoires des particules.

5
c) Potentiel électrique. Le potentiel électrique est le travail W d’une force s’exercent sur une
particule de charge unitaire Q = 1 C qui se déplace entre deux points (A et A’) d’un champ
électrique E. La différence de potentiel entre A et A’ est de 1 volt [1 V], si la force s’exerçant
sur une charge électrique de 1 coulomb [1 C] effectue un travail de 1 joule [1 J] lorsque celle-ci
se déplace de A jusqu’à A’. Ceci se traduit par la relation suivante:
V [V] = W [J]/ Q [C] . (1.4)
où V = Vfinale – Vinitiale est la variation de potentiel entre la position finale et initiale.
Lorsqu'une différence de potentiel est appliquée aux bornes d'un condensateur, des
charges s'accumulent sur les deux armatures en quantités égales mais avec leur polarité opposée
(Fig. 1.3).
Fig. 1.3. Le champ électrique entre les armatures d’un condensateur plan.
Un champ électrique est produit par les charges présentes sur les armatures du
condensateur, située à une distance d. Il y a une relation directe reliant ce champ électrique
(uniforme) E entre les armatures et la différence de potentiel V aux bornes du condensateur :
E = V / d (1.5)
1.1.2. Systèmes d’électrodes
Le champ électrique d’un séparateur électrostatique est créé entre deux ou plusieurs
électrodes, c’est à dire des pièces métalliques connectées à un générateur de haute tension, de
l’ordre de 50 kV.
a) Electrode cylindrique tournante. La particularité du séparateur électrostatique que nous
étudions est la présence d’une électrode cylindrique tournante, aussi appelée tambour, reliée à
la terre (Fig. 1.4). Les installations disposant de telles électrodes sont appelées séparateurs
électrostatiques à tambour. Elles servent le plus souvent à séparer des matériaux granulaires
conducteurs et isolants.
Cette électrode a un grand diamètre, entre 150 mm et 400 mm, selon le modèle. Elle peut
tourner à une vitesse variable de zéro à plusieurs centaines de tour/min. Les particules qui sont
déposées sur la surface de ce tambour sont donc soumises à des forces centrifuges variables,
qui ont un rôle très important dans le processus de séparation électrostatique.
E
V
d
+ + + + + + + + + + + +
+ + +
- - - - - - - - - - - - - - -

6
Fig. 1.4. Electrode cylindrique tournante
b) L’électrode couronne. Cette électrode a un très faible rayon de courbure ; cela veut dire
qu’elle se présente sous la forme d’un fil, d’une lame ou d’une pointe. Sur la figure 1.5, on
aperçoit une électrode qui comporte une ligne de pointes. Les zones lumineuses correspondent
aux régions de l’espace où se manifeste l’effet couronne.
Cette décharge lumineuse est l’aspect visible de l’effet couronne. Cet effet est lié à
l’ionisation de l’air dans la zone de champ électrique très intense produit à la surface d’une telle
électrode à faible rayon de courbure. Les particules soumises au flux d’ions générés dans une
décharge couronne négative, vont se charger négativement. Et ceci sera fondamental pour leur
trajectoire.
c) L’électrode statique. De la même façon que l’électrode couronne, celle-ci est liée à la haute
tension négative. C’est cette électrode qui, par sa forme et sa position, créé le champ électrique
intense nécessaire à la séparation.
L’électrode statique montrée sur la figure 1.6 a une section transversale ellipse. Celle-ci
assure une plus grande uniformité au champ électrique crée par rapport à l’électrode
cylindrique reliée à la terre, comme le montre les lignes équipotentielles représentées sur la
figure 1.7.
Fig 1.5. Electrode couronne à pointes.

7
1.1.3. Comportement des particules dans un séparateur électrostatique a tambour
Dans un séparateur électrostatique à tambour (Fig. 1.8), le champ électrique est créé entre
deux électrodes (1) et (2) connectées au générateur haute tension et l’électrode tournante reliée
à la terre (3). La goulotte oscillante (4) dépose le produit granulaire à séparer sur la surface de
l’électrode (3), qui l’introduit dans la zone du champ électrique. Deux mécanismes de charge
sont simultanément employés: "bombardement ionique", produit par l’électrode couronne, et
"induction électrostatique". Le premier est destiné aux particules isolantes ; le deuxième
implique seulement les particules conductrices. La charge acquise par les granules isolants dans
la zone de décharge couronne détermine la valeur de la force électrique qui les « collent » sur la
surface du tambour relié à la terre. Les granules isolants tombent dans la partie du collecteur
qui leur est réservée lorsque la résultante des forces de pesanteur et centrifuge l’emportent sur
la force électrique.
Fig. 1.6. L’électrode statique d’un séparateur à tambour.
Décharge
couronne à
partir d
’une
électrodes à
pointes
Electrode
statique à
section
transversale
ellipse
Câble haute
tension
Electrode
cylindrique
tournante liée
à la terre
Lignes
équipotentielles
Electrode
cylindrique
tournante
liée à la
terre
V = 0
V = 40 kV
Fig. 1.7. Lignes équipotentielles calculées avec un logiciel
d’analyse numérique du camp électrique.