Paramètres S Analyseur de réseaux Amplification de puissance

Dept. GEII IUT - Université Bordeaux1
Paramètres S
Analyseur de réseaux
Amplification de puissance
G. Couturier
[email protected]

2
Sommaire
I- Introduction : modèle physique versus modèle comportemental
I-1- Paramètres physiques
I-2- Modèle physique simplifié de la diode et schéma aux petits signaux
I-3- Modèle physique simplifié du transistor et schéma aux petits signaux
I-4- Deux diodes tête bêche : un transistor ?
I-5- Modèle physique du transistor et schéma aux petits signaux
I-6- Paramètres comportementaux
I-7- Relation entre paramètres H et paramètres physiques
II- Les paramètres S d'un quadripôle
II-1- Signification physique des paramètres S
II-2- Relation entre paramètre S et paramètres H
II-3- Etude de cas : un transistor et un amplificateur
III- Principe de fonctionnement d’un analyseur de réseaux
III-1- L’analyseur de réseaux vectoriel HP8753D
III-2- Correction des erreurs
IV- Paramètres S et amplification de puissance
IV-1- Gain en puissance d’un quadripôle unilatéralisé
IV-2- Adaptation d’impédance : cas d’un quadripôle unilatéralisé
IV-3- Exemple de quadripôle unilatéralisé
IV-4- Gain en puissance d’un quadripôle réel
IV-5- Exemple de quadripôle réel : cercles de stabilité
a) adaptation simultanée, K>1
b) adaptation simultanée impossible, K<1, cercles de stabilité
c) adaptation en bruit

3
V- Adaptation d’impédance
V-1- Puissance déposée dans une charge : condition d’adaptation
V-2- Circuit d’adaptation
V-3- Adaptation d’une source à une charge via un câble
V-4- Exemple de calcul du réseau d’adaptation par logiciel
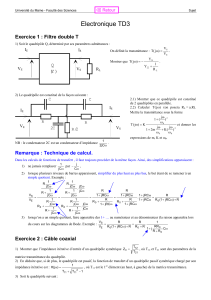
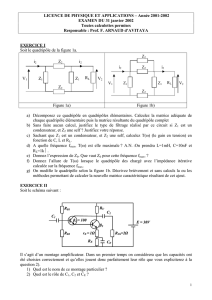
Exercice n°1 : Matrice Y de deux quadripôles en parallèle
Exercice n°2 : Paramètres S d’un quadripôle adaptateur
Exercice n°3 : L’amplificateur AD8354 1MHz – 2,7GHz
Exercice n°4 : Pont de mesure des paramètres 11
S et 22 S
Exercice n°5 : Coupleur latéral pour la mesure des paramètres 11
S et 22 S
Exercice n° 6 : Adaptation d’impédance et câble de transmission
Annexe 1 : Caractéristiques techniques des diodes BAW78 et BAS16
Annexe 2 : Caractéristiques techniques du transistor MRF104T1
Annexe 3 : Calcul du paramètre 12
S en fonction des paramètres H
Annexe 4 : Caractéristiques techniques de l’amplificateur AD8354
Annexe 5 : Corrections des erreurs pour la mesure des paramètres 11
S et 22 S
Annexe 6 : Corrections des erreurs pour la mesure des paramètres 21
S et 12 S
Annexe 7 : Gain en puissance d’un quadripôle unilatéralisé
Annexe 8 : Facteur de bruit NF d’un quadripôle
Annexe 9 : Matrice chaîne d’un tronçon de ligne

4
Pré requis : cours de propagation, coefficient de réflexion, rapport d’onde stationnaire,
abaque de Smith
Mots clés : modèle physique et comportemental, paramètres S, analyseur de réseaux,
correction des erreurs, détection synchrone
Le transistor bipolaire fut découvert en 1947 par J. Bardeen, W. H. Brattain et W. B.
Schockley des Laboratoires Bell Telephone. Pour cette découverte, ils reçurent le prix Nobel
en 1956. J. Bardeen obtint un second prix Nobel en 1972 avec L. N. Cooper et J. R. Schrieffer
pour la théorie de la Supraconductivité, théorie connue sous le nom de BCS.
I- Introduction : modèle physique versus modèle comportemental
I-1- Paramètres physiques
D’une manière générale, on a besoin en électronique de disposer de modèles des
composants pour faire de la simulation, c'est-à-dire prédire le comportement d’un montage
faisant appel à plusieurs composants. Il faut comprendre le mot composant au sens large, ça
peut être un simple transistor mais aussi un circuit intégré amplificateur comportant une
dizaine de transistors.
On dispose soit de modèles physiques soit encore de modèles comportementaux. Par
modèle physique, il faut comprendre un ensemble d’équations régissant le fonctionnement
physique du composant.
I-2- Modèle physique simplifié de la diode et schéma aux petits signaux
L’équation reliant le courant D I à la tension D V dans une diode, )e1(II kT/
D
qV
SD −= ,
est une équation déduite de la physique des semiconducteurs. Ce modèle physique simplifié
fait apparaître un seul paramètre : le courant de saturation S
I, C10.6,1q 19− = est la charge
de l’électron, K/J10.38,1k 23−
= est la constante de Boltzmann et T est la température en
degré Kelvin. Un modèle un peu plus élaboré donne : )e1(II NkT/)
D
I
s
R
D
V(q
SD −
−= où
s
R est la résistance série de la diode et N le facteur d’idéalité, en pratique s R est de l’ordre
de l’Ohm et 2N1 << . L’effet de la résistance s
R se manifeste aux forts courants quand
DsIR devient du même ordre de grandeur que D
V. Les modèles physiques ci-dessus ne
permettent pas de prédire le comportement en fonction de la fréquence ni de prédire le
courant de bruit. Pour s’en convaincre, il suffit de faire l’expérience de la figure 1 : une f.e.m.
E, un générateur sinusoïdal )tsin(Ae
ω
= de fréquence f variable et une diode D. On fait les 3
expériences suivantes :
• 0e =, la tension D
V aux bornes de la diode est une tension continue égale à 0D V.
0D
V est obtenue en résolvant l’équation
(
)
0D
kT/
0D
qV
SV1eRIE +−= pour le modèle plus
simple. Le courant D
I passant dans la diode est un courant continu égal à 0D I :
−= 1eII 0D
V
kT
q
S0D .
• )tsin(Ae ω= avec une basse fréquence f et une faible amplitude A, dans ce cas la
tension aux bornes de la diode est la somme d’une composante continue 0D
V et d’une
tension sinusoïdale de fréquence f en phase avec la tension e du générateur. La tension V aux

5
bornes est obtenue en résolvant
(
)
D
kT/
D
qV
SV1eRI)tsin(AE +−=ω+ . Si l’amplitude A est
faible, la tension D
V n’est pas très différente de 0D V et on écrit que vVV 0DD += .
()
vV1eeRIvV1eRI)tsin(AE 0D
v
kT
q
0D
V
kT
q
S0D
v
0D
V
kT
q
S++
−=++
−=ω+ +
Si la tension v est faible on peut remplacer
v
kT
q
e par son développement limité
...v
kT
q
2
1
v
kT
q
1e 2
2
v
kT
q
+ ++≈ . Si 2
2
v
kT
q
2
1
v
kT
q
>> , c'est-à-dire q
kT2
v<< ou
encore mV50v << , alors seul le premier terme du développement est à retenir :
v
kT
q
1e
v
kT
q
+≈ , c’est ce que l’on appelle l’approximation linéaire ; on a linéarisé
l’exponentielle. On obtient donc :
vV1v
kT
q
1eRI)tsin(AE 0D
0D
V
kT
q
S++
−
+=ω+ avec :
(
)
0D
kT/
0D
qV
SV1eRIE +−=
d’où : vv
kT
q
eRI)tsin(A 0D
V
kT
q
S+=ω ou encore :
0D
V
kT
q
Se
kT
qI
R1
)tsin(A
v
+
ω
=
La quantité 0D
V
kT
q
Se
kT
qI est homogène à l’inverse d’une résistance, en effet si on écrit
l’équation aux dimensions, on obtient : S
CV
CA
KJK
CA
e
kT
qI 1
1
0D
V
kT
q
S=Ω===
−
−, posons
D
0D
V
kT
q
S
r
1
e
kT
qI =. La tension v s’écrit alors :
e
rR
r
)tsin(A
rR
r
r
R
1
)tsin(A
e
kT
qI
R1
)tsin(A
v
D
D
D
D
D
0D
V
kT
q
S
+
=ω
+
=
+
ω
=
+
ω
=
La résistance D
r est égale à l’inverse de la pente de la caractéristique )V(fI DD =
calculée au point )V ,I( 0D0D , voir la figure 2. C’est la résistance dynamique de la diode.
Vérifions le en calculant
0D
V,
0D
I
D
D
dV
dI , il vient :