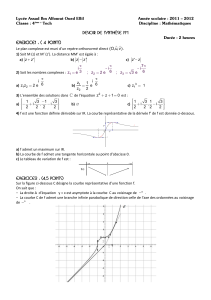
Maths pour la TB1

Lycée Ozenne, Toulouse Rentrée 2013
Site d’Auzeville
Mathématiques
pour l’entrée en classe de
TB1
Travail à imprimer et à effectuer pour la rentrée 2013.

Mathématiques à l’usage des étudiants
admis en classe préparatoire
Technologie-Biologie 1ère année
Travail à imprimer et à effectuer pour la rentrée.
Vous êtes admis en classe de TB1.
L’expérience prouve que les mathématiques sont souvent la matière qui donne le plus de difficultés
à l’étudiant de TB1. La raison principale est que les lycéens ont négligé ou peu travaillé cette matière
et ils ont en plus oublié les techniques élémentaires de calcul (tables de multiplication, calculs avec
fractions, exposants, factorisations, valeurs absolues...)
Pour faciliter la transition avec la prépa et prévenir peut-être quelques déconvenues, nous vous
demandons un sérieux travail de remise à niveau à effectuer avant la rentrée.
Profitez du répit de ces grandes vacances pour assurer les techniques élémentaires de calcul : l’ad-
dition et le produit de fractions, les inégalités, la valeur absolue, la racine carrée, les identités remar-
quables, la factorisation des polynômes. Toutes ces notions doivent être maîtrisées.
Revoyez aussi dans votre programme de terminale la partie analyse, c’est celle qui porte sur les
fonctions numériques (limite, dérivée, primitive, les fonctions ln,exp, puissances, du type x7→ xαoù
αest un réel, et leur propriétés.)
Il n’y a pas de statistiques cette année en cours de mathématiques, nous étudierons ensemble les
probabilités.
Voici un fascicule pour vous guider dans votre travail. Travaillez-le c’est-à-dire : apprenez les
définitions puis cherchez les exemples et les exercices. Ne vous contentez pas d’une lecture superficielle,
et ne vous arrêtez pas à la première difficulté.
Dès le début de l’année, l’acquis de cete opuscule sera utilisé et exploité en mathématiques.
Un contrôle sur les exercices  1à 18 sera effectué à la rentrée.
De plus je vous demande de faire une fiche détaillée sur les fonctions ln et exp : définitions, dérivées,
limites, tableaux de variations, courbes.
Maintenant permettez-moi de vous souhaiter de bonnes vacances... quelque peu studieuses et j’es-
père vous trouver en bonne forme pour la rentrée.
J.-M. Pierre

Première partie
Notions élémentaires
I. Identités remarquables
Ecrire les identités remarquables :
(a+b)2= (a−b)2=
a2−b2=Ne pas confondre (a−b)2et a2−b2!
Développer :
(a+b)3=
(a−b)3=
(a−b)(a2+ab +b2) =
Factoriser :
x2−1 = x3−1 =
1−x2=
1
On rappelle que si un polynôme s’annule pour une valeur α, alors il est factorisable par (x−α).
Exemple : x2−x−2s’annule pour x=−1, donc x2−x−2=(x+ 1)( ? ), la parenthèse ( ? )
est facile à trouver, c’est (x−2).
Factoriser de cette façon x2−3x+ 2 (on commence par chercher une valeur “évidente” qui annule 2
le polynôme, en envisageant 1, −1, 2, −2) et x2−x−6.
II. Quantité conjuguée
Exemple : la quantité conjuguée de √5 + √3est √5−√3, la quantité conjuguée de 2−√3est
2 + √3. Son emploi dans les fractions permet de supprimer les signes √au dénominateur.
1
√5 + √3=√5−√3
(√5 + √3)(√5−√3) =√5−√3
5−3=1 2(√5−√3).
1
2−√3=2 + √3 (2 −√3)(2 + √3) =2 + √3
4−3= 2 + √3.
1
3√3−2√7=
1

III. Valeur absolue
La valeur absolue d’un nombre réel xest la distance de xà 0, elle est notée |x|. Par exemple la
distance de −2à 0 est 2, donc | − 2|= 2.
On remarque que | − 2|=−(−2), ce qui est vrai pour tout les réels négatifs.
A savoir :
•|x|=xsi x≥0et |x|=−xsi x≤0.
•On a toujours |x| ≥ 0, et |x|= 0 ⇐⇒ x= 0.
•| − x|=|x|
•|xy|=|x||y|
•
x
y
=|x|
|y|
•|x+y| ≤ |x|+|y|
•Si a≥0alors on a : |x| ≤ a⇐⇒ −a≤x≤a. Exemple : |x| ≤ 1⇐⇒
donc |x|> a ⇐⇒ (x > a ou x < −a).
•|x|=|y| ⇐⇒ (x=you x=−y)
•√x2=|x|alors que (√x)2=x. Exemple : (−3)2=
•|x|2=x2.
2