Loi Normale - MathsAuLycee

La loi normale.
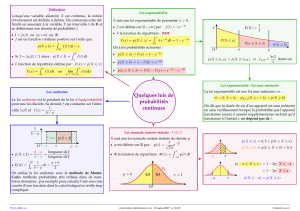
Identification d'une distribution normale.
On
dit qu'une série statistique suit une loi normale lorsque
sa
fonction de distribution a une forme
en
cloche centrée sur la moyenne.
(m
sur
la
figure ci-dessous).
La
loi normale permet de calculer les probabilités p(X <x) d'une variable continue.
Loi
Normale
m
Exemple: On a relevé le poids des enfants d'une même classe d'âge (variable x).
On
représente les
valeurs de cette variable par un diagramme en bâtons(
en
prenant les centres des classes):
!POIds
!centre
de
la
classe Effectif
•25-26[ i 25,5 3
1[26-27[
26,5
7·
1[27-28[
27,5 18
1[28-29[
28,5 401

120
100
80
60
40
20
o
~
~ ~ ~
~
~ ~
~ ~
~ ~
~~
<.o~
"'~
<:o~
O')~
c:r
"""
C'\I~
(lt'f
~~
~~
C'\I C'\I
C'\I
C'\I
C'\I
~ ~ ~
~
~
~
La
distribution "Poids des enfants" peut être qualifiée de normale.
Caractéristiques
d'une
distribution normale
Les trois caractéristiques de tendance (moyenne, mode et médiane) sont sensiblement égales.
Sensiblement 68% des observations sont comprises dans l'intervalle m+/-
0"
.
Sensiblement 95% des observations sont comprises dans l'intervalle
m+/-20"
.
Retour à l'exemple:
Les calculs montrent que:
La moyenne m est égale à 30,505.
La médiane est égale à 30,5.
Le mode (centre de la classe modale) est égal à 30,5.
La variance est égale à 2,94, donc
0"
= 1,715.
L'intervalle m+/-
0",
c'est à dire [28,79; 32,22] contient 69,48% des observations.
L'intervalle
m+/-20",
c'est à dire [27,07; 33,94] contient 94,87% des observations.
Toutes les conditions requises pour supposer une distribution normale sont vérifiées.
Paramètres
de la loi normale
La moyenne ( espérance) et l'écart type calculés sur la série statistique constituent les paramètres de
la loi normale:
X----tt-
N(m;
0"
).
Soit la variable X de l'exemple précédent: X
----tt-
N(30,505 ; 1,715).

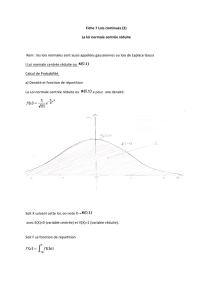
Calculs de probabilités
par
la loi normale
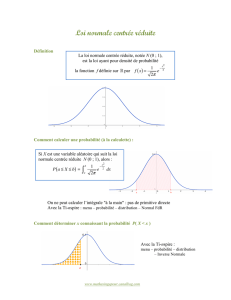
La
loi normale centrée réduite
Une variable dont la distribution satisfait aux critères de normalité, est réputée suivre une loi
normale de paramètres m et
(J
(caractéristiques calculées sur la série statistique).
Une variable suit une loi normale centrée réduite si sa moyenne est égale à 0
et
son écart type à
1.
Si
X
suit
une
loi
normale
de
paramètres
m
et
0'
alors
la
variable
T=
X-m
suit
une
loi
normale
(J
centrée réduite. Ainsi p(X<x)=p(T<t).
L'intérêt d'un tel changement de variable est qu'il existe des tables de la loi normale centrée réduite.
(cf
annexe).
Exemple: Le kilométrage moyen annuel réalisé par les conducteurs de véhicule essence suit une loi
normale de moyenne 15000 et d'écart type 6000. Soit X la variable aléatoire représentant le nombre
de kilomètres parcourus par un véhicule.
X----iI>
N(15000,6000).
T
X~l;oOoOO
et
T----iI>N(O,l)
On
cherche la probabilité qu'un véhicule parcourt moins de 25000
km
par an.
25000-15000
p(X<25000)=p(T< 6000 )=p(T<I,67).
Par lecture de la table
de
la loi normale centrée réduite: peT <1,67)=0,9525.
Propriétés
1
p(T>t)=l-
p(T<t) p(T< -t)=p(T> t)
Applications:
1.
La durée de fonctionnement sans panne d'un type de machine est en moyenne de 950
heures avec un écart type de 100 heures.
X=durée de fonctionnement.
x-+
N(950;100) et T
----il>N(O;I)
.
• Quelle est la probabilité pour que la première panne survienne, sur l'une des machines,
après plus de 1000 heures
de
fonctionnement?
• Quelle est la probabilité pour que la première panne survienne avant 850 heures de
fonctionnement.
• Quelle est la probabilité pour que la première panne survienne entre 900 et 1000 heures
de fonctionnement.
2. Le poids X en grammes d'un cèpe suit une loi normale N(60;3).
Calculer
p(57<X~61)
3.
On
sait que X suit une loi normale de paramètres m et
(J
. En sachant que
p(X~0,5)=0,5517
et
P(X~2,6)=0,9515,
déterminer m et
(J,
1
/
3
100%