là - CPGE Brizeux

fRf(x) = 3
√x+x3
f
f
f′(x)x f
f
f
fR
f
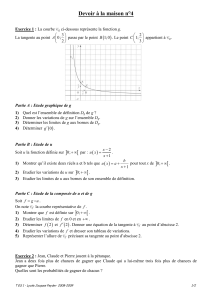
Cff
Cf
Cf+∞Cf+∞
Cf
(un)n∈Nu0>0un+1 =3
√un+u3
n
n∈N
(un)n∈N
un−→
n→+∞+∞
(un)n∈N
un+1 ∼
n→+∞un
un+1 −un∼
n→+∞
1
3un
1
un
f:R3−→ R3
(x, y, z)7−→ (x+ 4y+ 6z, x +y+ 3z, −x−2y−4z)
f
f◦f=−f
⃗u ∈R3
⃗u ∈Imf⇐⇒ f(⃗u) = −⃗u.
Ker(f) Im(f)
f
(⃗e1, ⃗e2, ⃗e3) Ker(f)
Im(f)
(⃗e1, ⃗e2, ⃗e3)R3
Ker(f) Im(f)R3

k k
◃ A
◃ B
n>3
k∈J1, nK
◃ Akk A
◃ akAk
k∈J1, nKak+1 ak
(Ak, Ak)
an
n