∫ ∫ - Canalblog

1
Variable aléatoires utilisées
Trois types de variables aléatoires discrètes (prenant un nombre fini de valeurs) sont utilisées.
Les variables dépendent des deux paramètres n et p.
Par exemple, on lance n fois une pièce déséquilibrée pour laquelle la probabilité d’obtenir
« pile » est égale à p = 0,6.
La variable aléatoire X n est égale au nombre de fois où on obtient « pile ».
Les variables aléatoires X n suivent des lois binomiales de paramètres n et p.
La variable aléatoire X n prend les valeurs entières de 0 à n, E(X) = n p et
( ) (1 )
X n p p
.
La variable aléatoire Z n est la variable aléatoire centrée-réduite associée à X n. La variable
aléatoire Z n prend des valeurs discrètes, souvent non entières, E(Z n ) = 0, (Z n ) = 1
Toutes les variables Z n ont la même espérance et le même écart-type mais elles sont différentes
(les valeurs prises par Z n dépendent de n et de p).
La variable aléatoire
n
n
X
F
n
 est la variable aléatoire qui est la fréquence associée à X n. La
variable F n prend des valeurs discrètes dans [ 0 ; 1 ]
E(F n ) = p (indépendante de n) et (F n ) diminue quand n augmente.
Centrer et réduire
Définition : Une variable aléatoire est centrée et réduite lorsque son espérance est nulle et son
écart-type égal à 1.
Propriété : Soit X une variable aléatoire d’espérance m et d’écart-type , la variable aléatoire
X m
Z est une variable aléatoire centrée et réduite.
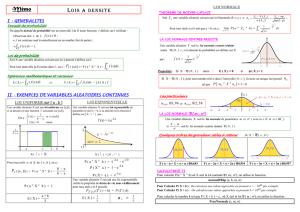
Théorème de Moivre-Laplace
Soit p un nombre réel de l’intervalle ] 0 ; 1 [.
Soit une suite de variables aléatoires (X n ) où chaque variable aléatoire X n suit la loi binomiale
B (n ; p ).
On pose
(1 )
n
n
X n p
Z
n p p
, variable centrée et réduite associée à X n , alors, pour tous réels a
et b tels que a < b, on a :
2
2
1
lim ( ) e d
2
x
b
n
na
P a Z b x
Loi normale centrée réduite
Définition : Une variable aléatoire X suit la loi normale centrée réduite N (0 ; 1) si, pour tous
réels a et b tels que a < b, on a :
2
2
1
( ) e d
2
x
b
a
P a X b x
.
Si X suit la loi normale N (0 ; 1) alors E(X) = 0 et (X) = 1.

2
Lorsque la variable aléatoire X suit la loi normale N (0 ; 1), pour tout nombre  de l’intervalle
] 0 ; 1 [, il existe un unique nombre réel positif u  tel que P( – u  ≤ X ≤ u  ) = 1 – 
Valeurs particulières à connaître :
u 0,05 ≈ 1,96 d’où : P(– 1,96 ≤ X ≤ 1,96) = 0,95
u 0,01 ≈ 2,58 d’où : P(– 2,58 ≤ X ≤ 2,58) = 0,99
Autres lois normales
Définition : Une variable aléatoire X suit une loi normale N (µ ;  2 ) si la variable aléatoire
X
Z suit la loi normale centrée réduite N (0 ; 1).
Espérance et écart-type
Si une variable aléatoire X suit la loi normale N (µ ;  2 ) alors E(X) = µ et (X) = 
Calculs
La variable aléatoire X suivant la loi normale N (µ ;  2 ), il faut savoir calculer des probabilités
de la forme : P( a ≤ X ≤ b), P (X ≤ c) et P (X  c), a, b et c étant des nombres réels donnés.
Il faut aussi savoir déterminer le nombre x tel que P(X ≤ x) = p, p étant une probabilité donnée.
A connaitre :
P(µ –  ≤ X ≤ µ + ) ≈ 0,68 (à 10 – 2 près)
P(µ – 2  ≤ X ≤ µ + 2 ) ≈ 0,95 (à 10 – 2 près)
P(µ – 3  ≤ X ≤ µ + 3 ) ≈ 0,997 (à 10 – 3 près)

3
Intervalles de fluctuation
Définition : Un intervalle de fluctuation asymptotique de la variable aléatoire
n
n
X
F
n
 au
seuil 1 –  (ou avec le risque ) est un intervalle déterminé à partir de p et de n et qui contient
F n avec une probabilité d’autant plus proche de 1 – que n est grand.
Théorème
Soit p un nombre réel fixé de l’intervalle ] 0 ; 1 [.
Soit une suite de variables aléatoires (X n ), chaque variable aléatoire X n suivant la loi binomiale
B(n ; p ), alors, pour tout réel  dans ] 0 ; 1 [, on a lim 1
nn
n
X
P I
n
  où I n est
l’intervalle
(1 ) (1 )
;
np p p p
I p u p u
n n
et u  désigne l’unique réel tel
que P( – u  ≤ Z ≤ u  ) = 1 – , la variable aléatoire Z suivant la loi normale N (0 ; 1).
Propriété : L’intervalle
(1 ) (1 )
;
np p p p
I p u p u
n n
est un intervalle de
fluctuation asymptotique au seuil 1 –  de la variable aléatoire
n
n
X
F
n
.
En particulier, l’intervalle
(1 ) (1 )
1,96 ; 1,96
np p p p
J p p
n n
est un
intervalle de fluctuation asymptotique au seuil de 95 %.
Conditions d’utilisation
Les exigences habituelles de précision pour utiliser cette approximation sont : n  30, n p  5 et
n p (1 – p )  5
Il faut savoir utiliser un intervalle de fluctuation pour prendre une décision.
La règle de décision adoptée étant la suivante :
Si la fréquence observée f dans un échantillon appartient à un intervalle de fluctuation
asymptotique au seuil de 95 %, on considère que l’échantillon est compatible avec le modèle ;
sinon, on considère que l’échantillon n’est pas compatible avec le modèle.

4
Méthode :
1. Enoncer l’hypothèse
2. Vérifier les conditions
3. n  30, n p  5 et n (1 – p)  5,
4. Déterminer l’intervalle de fluctuation
5. Arrondir la borne inférieure à 10 – 3 par défaut et la borne supérieure à 10 – 3 par excès.
(10 – 3 est un exemple)
6. Appliquer la règle de décision
Intervalle de confiance
Un intervalle de confiance (on dit aussi une « fourchette de sondage ») pour une proportion p à
un niveau de confiance de 95 % est la réalisation, à partir d’un échantillon, d’un intervalle
aléatoire contenant la proportion p avec une probabilité supérieure ou égale à 95 %.
Définitions
Il faut savoir estimer une proportion inconnue p grâce à un échantillon :
la proportion p est estimée par la fréquence f obs , l’intervalle obs obs
1 1
;f f
n n
  étant
un intervalle de confiance au niveau de 95 %.
Conditions d’utilisation
On se place dans le cas où l’échantillon contient au moins 30 éléments et où la fréquence f
observée est telle que n  30, n f obs  5 et n (1 – f obs )  5,
La précision de l’estimation est donnée par l’amplitude de l’intervalle
obs obs
1 1
;f f
n n
  qui est égale à 2
n et dépend donc de la taille n de l’échantillon.