Chapitre 15 : ORDRE et OPÉRATIONS.

Chapitre 15 : ORDRE et OPÉRATIONS.
I. Notations et définition.
Exemples :
x < 75 signifie que « x est strictement inférieur à 75 »
x > 125 signifie que « x est strictement supérieur à 125 »
x > 0 signifie que « x est strictement positif »
a  -23 signifie que « a est inférieur ou égal à -23 »
a b signifie que « a est supérieur ou égal à b »
Définition :  : < ; > ;  et 
II. Rappels (6ème) : troncature, arrondi.
On considère le nombre 3,57.
3,57 peut être encadré par deux nombres ayant un chiffre après la virgule et dont la différence est un dixième :
3,5 3,6
La troncature au dixième de 3,57 est celui de ces deux nombres qui est inferieur ou égal à 3,57.
La troncature au dixième de 3,57 est 3,5.
3,6.
Application : Compléter les tableaux ci-dessous :
NOMBRE
5,123
7,987
4,183
35,9271
78,096
NOMBRE
5,123
7,987
4,183
35,9271
78,096
TRONCATURE
AU CENTIEME
5,12
7,98
4,18
35,92
78,09
TRONCATURE
AU DIXIEME
5,1
7,9
4,1
35,9
78,0
ARRONDI AU
CENTIEME
5,12
7,99
4,18
35,93
78,10
ARRONDI AU
DIXIEME
5,1
8,0
4,2
35,9
78,1
III. Signe d’une différence.
Activité :
1) Effectuer à la calculatrice : 
  9,57×10-4
2) Compléter : 
 <   .
On conjecture la propriété suivante :
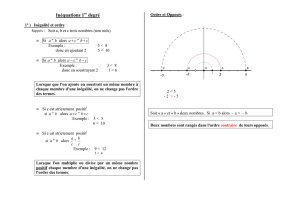
Si a – b < 0, alors a < b.
La réciproque est vraie :
Si a < b alors a – b < 0.
Remarque : Ces propriétés sont vraies avec les trois autres symboles 

IV. Ordre et opérations.
1) Ordre et addition – Ordre et soustraction.
Activité :
a) On a : 2 < 8
Donc : 2 + 3 < 8 + 3 et 2 – 7 < 8 – 7
b) On a : –11 < –7
Donc : –11 + 5 < –7 + 5 et –11 – 5 < –7 – 5
On peut conjecturer la propriété suivante :
a, b, c désignent trois nombres relatifs.
Les nombres a + c et b + c sont rangés dans le même ordre que les nombres a et b.
Par exemple : Si a < b, alors a + c < b + c
Applications : Compléter par < ou > :
x + 7,09 > x + 7,009 x  1,02 < x  1,002 
  >    3,14
2) Ordre et multiplication.
Exemple :
2 < 3 donc 52 < 53 mais -52 > -53
On peut conjecturer les propriétés suivantes :
a, b, c désignent des nombres relatifs.
 Lorsque c est strictement positif, les nombres a c et b c sont rangés dans le même ordre que les
nombres a et b.
Par exemple : Si a < b alors a×c < b×c
 Lorsque c est strictement négatif, les nombres a c et b c sont rangés dans l’ordre contraire des
nombres a et b.
Par exemple : Si a < b alors a×c > b×c
Autrement dit :
- On ne change pas le sens d’une inégalité lorsqu’on multiplie (ou lorsqu’on divise) par un même nombre
strictement positif les deux membres de cette inégalité.
- On doit changer le sens d’une inégalité lorsqu’on multiplie (ou lorsqu’on divise) par un même nombre
strictement négatif les deux membres de cette inégalité.

Exemples :
a et b désignent des nombres.
1) Si a < 5 alors 2a < 2×5 donc 2a < 10
2) Si a  3 alors -5a  -5×3 donc -5a -15
3) Si b  -4 alors b
2  
 donc b
2  -2
4) Si b > 3 alors b
-2 < 
 donc  b
2 < -1,5
V- Résolution d’une inéquation.
Résoudre une inéquation, c’est trouver toutes les valeurs de l’inconnue qui rendent vraie l’inégalité.
les solutions de l’inéquation.
grâce aux propriétés ci-dessus.
Exemple : –3x + 4  -2
–3x  –2 – 4 –3x  – 6 x ≤ 
 x ≤ 2
Les solutions de l’inéquation –3x + 4  –2 sont tous les nombres inférieurs ou égaux à 2.
Cette représentation consiste à tracer un axe gradué et orienté sur lequel on souligne les parties représentant les
nombres qui sont solutions.
 : –3x + 4  -2
Solutions
2
Applications :
a) 5x - 10  0
5x  10 donc x  2
b) 8x - 24 < 0
8x < 24 donc x < 3
c) 12 - 6x < 0
- 6x < - 12 donc x > 2
Les solutions de l’inéquation 12 - 6x < 0 sont tous les nombres strictement supérieurs à 2.
2
Solutions
3
Solutions
2
Solutions
Les solutions de l’inéquation 5x - 10 0 sont tous les nombres supérieurs ou égaux à 2.
Les solutions de l’inéquation 8x - 24 < 0 sont tous les nombres strictement inférieurs à 3.