Fiche Formules-et-theoremes - Arithmétique et fractions

19/05/2015 09:33Fiche Formules-et-theoremes - Arithmétique et fractions - Mathématiques 3ème - Afterclasse
Page 1 sur 4http://www.afterclasse.fr/#!fiche/72/arithmetique-et-fractions/cours-1
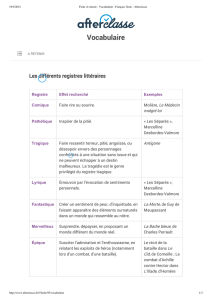
Arithmétique et fractions
A
Rappel
Écritures décimale et fractionnaire
L’écriture décimale d’un nombre fait apparaître sa partie entière (avant la virgule) et
sa partie décimale (après la virgule).
Ex. : 1, 20 ; 2 ; 34, 54 et 562, 536 sont des écritures décimales de nombres.
L’écriture fractionnaire d’un nombre est sa représentation sous la forme d’un
quotient de deux nombres.
Ex. : 0, 5 s’écrit aussi , qui est une écriture fractionnaire.
Définition
Entier relatif
Un entier relatif est un nombre (positif ou négatif) dont l’écriture décimale ne
comporte que des zéros après la virgule.
Exemple
2 ; −6, 0 ; −23, 0000 et 214 sont des entiers relatifs.
1ENTIERS RELATIFS ET NOMBRES RATIONNELS
Les entiers relatifs
2
1
Ads by macshopAd Options

19/05/2015 09:33Fiche Formules-et-theoremes - Arithmétique et fractions - Mathématiques 3ème - Afterclasse
Page 2 sur 4http://www.afterclasse.fr/#!fiche/72/arithmetique-et-fractions/cours-1
Remarque
Un entier naturel est un donc un entier relatif positif.
B
Définition
Nombre rationnel
Un nombre rationnel q est un nombre qui peut s'écrire comme le quotient de deux
entiers relatifs a et b avec b non nul.
On écrit q= , b≠0
Exemple
0, 5 est un nombre rationnel car il peut s'écrire sous la forme .
Il admet une infinité d'écritures fractionnaires : il peut s'écrire , , , etc.
−3 est un nombre rationnel car il peut s'écrire sous la forme .
Propriété
Périodicité de l’écriture décimale d’un nombre rationnel
L’écriture décimale d’un nombre rationnel est infinie, mais périodique.
Cela signifie « qu'au bout d'un moment », la partie décimale d'un nombre rationnel se
répète à l'infini.
Les nombres rationnels
b
a
2
1
2
1
4
2
6
3
1
−3

19/05/2015 09:33Fiche Formules-et-theoremes - Arithmétique et fractions - Mathématiques 3ème - Afterclasse
Page 3 sur 4http://www.afterclasse.fr/#!fiche/72/arithmetique-et-fractions/cours-1
Exemple
= 1 = 1, 0000... où 0 se répète à l'infini.
= 0, 5 = 0, 50000... où 0 se répète à l'infini.
= 0, 333333... où 3 se répète à l'infini.
= 0.142857142857142857... où 142857 se répète à l'infini.
Remarque
Les entiers relatifs sont des nombres rationnels.
Plusieurs couples (a;b) peuvent représenter le même nombre rationnel.
Ex. : 0, 5 = = =
Remarque
Les nombres qui ne sont pas des nombres rationnels sont dits irrationnels. Ils se reconnaissent
car :
ils ne peuvent pas s'écrire sous la forme d'un quotient de deux nombres ;
leur partie décimale n'a pas de périodicité.
Ex. : π= 3, 1415926...
Ex. : = 1, 732050...
Remarque
1
1
2
1
3
1
7
1
2
1
4
2
20
10
√3

19/05/2015 09:33Fiche Formules-et-theoremes - Arithmétique et fractions - Mathématiques 3ème - Afterclasse
Page 4 sur 4http://www.afterclasse.fr/#!fiche/72/arithmetique-et-fractions/cours-1