M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés

M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés
2013
Concepteur du cours : Olivia MARTINELLI Page 1
Exercice 1 :
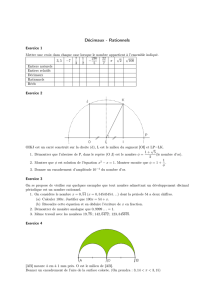
Préciser pour chacun de ces quatre nombres si ils sont entiers naturels,
décimaux, rationnels ou irrationnels.
Exercice 2 :
1. Donner deux rationnels non décimaux dont la somme est un entier.
2. Donner deux rationnels non décimaux dont le produit est un entier.
3. Donner deux décimaux non entiers dont le produit est un entier.
Exercice 3 :
Dans chacun des cas suivants trouver un nombre rationnel strictement compris
entre :
Exercice 4 :
Sans effectuer l’opération, expliquer pourquoi le nombre suivant est un
nombre décimal :

M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés
2013
Concepteur du cours : Olivia MARTINELLI Page 2
Exercice 5 :
Les nombres  et  ont pour produit 247 et pour somme 32.
1) Sans calculer et, trouver la valeur de :
2) Supposons que  et  soient des entiers, les déterminer en utilisant la
décomposition en produit de nombres premiers de 247.
Conclure sur leur appartenance ou non à l’ensemble des entiers naturels.
Vérifier alors les résultats obtenus à la question 1.
Exercice 6 :
1. Un spectacle dure 3 heures et 25 minutes. Exprimer la mesure de cette
durée, en prenant l'heure comme unité, sous forme d'une fraction irréductible.
Ce nombre est-il un décimal ?
2. Une mesure de durée est exprimée sous la forme heures et minutes
Pour quelles valeurs de  et la mesure en heures de la même durée sera-t-
elle exprimée par un nombre décimal ?
Exercice 7 :
1- On considère le rationnel dont l’écriture à virgule est  sa
période étant.
Ecrire ce rationnel sous la forme d’une fraction irréductible.
2- On considère le rationnel dont l’écriture à virgule est 
la période étant.
Ecrire ce rationnel sous la forme d’une fraction.

M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés
2013
Concepteur du cours : Olivia MARTINELLI Page 3
Exercice 8 :
1. Parmi les nombres rationnels suivants, quels sont ceux qui sont des
décimaux ?
Justifier la réponse.
2. Le but de cette question est d’étudier l’écriture décimale périodique de 
a. Poser la division de 1 par 7. En déduire l’écriture décimale périodique de
b. Donner, en justifiant, la 32ième décimale du développement périodique de

M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés
2013
Concepteur du cours : Olivia MARTINELLI Page 4
3. Le but de cette question est de produire l’écriture décimale périodique
de
. En utilisant le tableur pour effectuer la division de 42 par 17 on obtient
le tableau suivant. A partir de la cellule A2, la colonne A donne les restes
successifs de la division de 42 par 17. A partir de la cellule B2, la colonne B
donne les quotients successifs.
a. Donner sans justification la 20ième décimale de l’écriture décimale de
b. A partir du tableau ci-dessus donner l’écriture décimale périodique de 
c. Expliquer pourquoi on est sûr de retrouver dans la cellule A19 un reste déjà
obtenu.
4. On se propose maintenant de retrouver l’écriture fractionnaire du
rationnel. Pour cela, calculer  et en déduire
l’écriture de  sous forme fractionnaire.
Exercice 9:
1) Démontrer que : Si  et  sont des nombres décimaux alors la somme
 est un nombre décimal.
2) Démontrer que : Si  et  sont des nombres décimaux alors le produit
 est nombre décimal.
3) Démontrer que : Si  et  sont des nombres rationnels alors la somme
 est un nombre rationnel.
4) Démontrer que : Si  et  sont des nombres rationnels alors le produit
 est un nombre rationnel.

M1 S1 CH2 : Les ensembles de nombres : exercices : énoncés
2013
Concepteur du cours : Olivia MARTINELLI Page 5
Exercice 10 :
La lettre désigne un nombre. Dire en justifiant si les énoncés suivants sont
vrais ou faux.
Enoncé 1 : Si  est un nombre entier naturel, alors est un nombre entier
naturel.
Enoncé 2 : Si  est un nombre entier naturel, alors est un nombre
entier naturel.
Exercice 11:
Soit et  deux entiers naturel tels que :
Le nombre  est-il un nombre entier ?