Chapitre 3 Compléments sur les fonctions numériques

Chapitre 3
Compléments sur les fonctions
numériques
24

1) Compléments sur la dérivation
1 - 1) Dérivées des fonctions √uet un,n∈Z
Théorème :
Si uest une fonction strictement positive, dérivable sur un intervalle I,
alors la fonction √uest dérivable sur I, et pour tout xde I:
pu(x)0
=u0(x)
2pu(x)
Exemple :
f(x) = √x2+x+ 1 peut être vu comme u(x) = x2+x+ 1, avec f(x) = pu(x); au passage,
on peut vérifier que pour tout xde R,x2+x+ 1 >0.
D’après le théorème précédent, f0(x) = u0(x)
2pu(x)=2x+ 1
2√x2+x+ 1
Démonstration :
Soit aun réel appartenant à Iet hun réel tel que a+happartient à I.
Le taux d’accroissement de la fonction √uentre aet a+hest égal à :
τ(h) = pu(a+h)−pu(a)
h
En multipliant le numérateur et le dénominateur par pu(a+h) + pu(a)(c’est ce qu’on
appelle la quantité « conjuguée » de pu(a+h−pu(a)), on obtient :
τ(h) = u(a+h)−u(a)
h×1
pu(a+h) + pu(a)
uest continue en adonc : lim
h→0
1
pu(a+h) + pu(a)=1
2pu(a)
uest dérivable en adonc : lim
h→0
u(a+h)−u(a)
h=u0(a)
On obtient par produit de limites : lim
h→0τ(h) = u0(a)×1
2pu(a)
Ainsi, √uest dérivable en aet le nombre dérivé est égal à u0(a)
2pu(a)
Ceci étant vrai pour tout ade I, on conclut que √uest dérivable sur Iavec (√u)0=u0
2√u
25

Théorème :
nest un entier non nul.
Si uest une fonction dérivable sur un intervalle I, et si, lorsque nest
négatif, une s’annule pas sur I, alors la fonction unest dérivable sur I, et
pour tout xde I:
(un(x))0=n u0(x)un−1(x)
Exemple :
f(x) = (x2+x+ 1)3peut être vu comme u(x) = x2+x+ 1, avec f(x)=(u(x))3.
D’après le théorème précédent, f0(x)=3u0(x)u3−1(x) = 3 ×(2x+ 1)(x2+x+ 1)2
Démonstration :
Démonstration pour nentier naturel non nul :
Si uest la fonction nulle, ce résultat est bien vérifié. Sinon, on procède par récurrence.
uétant une fonction dérivable sur un intervalle I, on pose pour tout entier n>1,P(n):
«(un(x))0=n u0(x)un−1(x)»
Initialisation : pour n= 1,(u1)0=u0; d’autre part, 1×u0×u1−1=u0:P(1) est vraie.
Hérédité : supposons que pour p>1,P(p)est vraie (c’est l’hypothèse de récurrence).
Montrons maintenant que P(p+ 1) est vraie :
(up+1)0= (u×up)0=u0×up+u×(up)0(par dérivation d’un produit)
Cela donne, en utilisant l’hypothèse de récurrence :
(up+1)0=u0×up+p×u0up−1=u0×up+p u0up= (p+ 1) u0up
Cela montre que P(p+ 1) est vraie.
Conclusion : la proposition est vraie au rang 1, elle est héréditaire ; d’après le principe de
récurrence, P(n)est vraie pour tout entier n>1.
Démonstration pour nentier strictement négatif :
Il suffit de remarquer que un=1
u−net qu’alors, −nest un entier strictement positif.
On peut alors appliquer le résultat précédent à u−n; ainsi :
(un)0=1
u−n0
=−(u−n)0
(u−n)2=−(−n)u0u−n−1 u−2n=n u0u−n−1+2n=n u0un−1
On retrouve bien le résultat précédent.
26

1 - 2) Dérivée de x7→ f(ax +b)
Théorème :
fest une fonction dérivable sur R,aet bdeux nombres (a6= 0).
Alors la fonction g:x7→ f(ax +b)est dérivable sur R.
Sa dérivée g0est définie par g0(x) = af 0(ax +b)
Exemple :
g(x) = (2x+ 3)5peut être vu comme f(2x+ 3), avec f(X) = X5; on a alors f0(X) = 5X4
D’après le théorème précédent, g0(x)=2f0(2x+ 3) = 2 ×5(2x+ 3)4= 10(2x+ 3)4
Démonstration :
Pour tout nombre h6= 0, notons τ(h)le taux d’accroissement de gentre xet x+h:
τ(h) = g(x+h)−g(x)
h=f(a(x+h) + b)−f(ax +b) h
Posons ax +b=Xet ah =H; alors, τ(h) = a×f(X+H)−f(X)
H
Or, lim
h→0H= 0 et lim
H→0
f(X+H)−f(X)
H=f0(H), par dérivabilité de la fonction f.
D’après le théorème sur la limite d’une fonction composée,
lim
h→0
f(ax +b+ah)−f(ax +b)
ah =f0(ax +b)
Il en résulte que lim
h→0τ(h) = a×f0(ax +b). Ainsi, gest dérivable en x.
Ce résultat étant vrai pour tout nombre xde R,gest dérivable et g0(x) = af 0(ax +b)
27

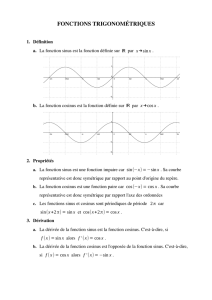
2) Les fonctions sinus et cosinus
2 - 1) Définitions et propriétés des fonctions sinus et cosinus
Définitions :
(1) La fonction sinus est la fonction qui, à tout réel x, associe sin(x).
(2) La fonction cosinus est la fonction qui, à tout réel x, associe cos(x).
Propriétés :
(1) Les fonctions sinus et cosinus sont continues sur R.
(2) Les fonctions sinus et cosinus sont dérivables sur R, et pour tout réel x:
sin0(x) = cos(x)et cos0(x) = −sin(x)
(3) La fonction fdéfinie sur Rpar f(x) = sin(ax +b)est dérivable sur R, et pour
tout réel x:
sin0(ax +b) = a cos(ax +b)
La fonction fdéfinie sur Rpar f(x) = cos(ax +b)est dérivable sur R, et pour tout
réel x:
cos0(ax +b) = −a sin(ax +b)
Pérodicité :
Pour tout réel x,sin(x+ 2π) = sin(x)et cos(x+ 2π) = cos(x)
On dit que les fonctions sinus et cosinus sont périodiques de période 2π.
Conséquence :
Pour tracer la courbe représentative de la fonction sinus, il suffit de la tracer sur un intervalle
d’amplitude 2π, puis de compléter par des translations successives de vecteur 2π~ iou −2π~ i.
Il en est de même pour la courbe représentative de la fonction cosinus.
28