Trigonométrie La trigonométrie est l`outil mathématique qui permet

Trigonométrie
La trigonométrie est l'outil mathématique qui permet de lier les angles aux longueurs.
La trigonométrie ne fonctionne que dans les triangles rectangles.
I – Formules de trigonométrie
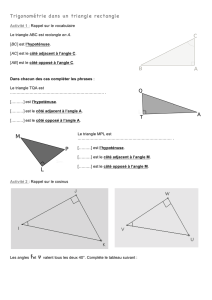
On utilisera le vocabulaire suivant :
Les formules sont :
cosinus=adjacent
hypoténuse
sinus=opposé
hypoténuse
tangente=opposé
adjacent
(moyen mnémotechnique : CAHSOHTOA)
Dans notre exemple, on a donc :
cos(
̂
A)= adjacent de
̂
A
hypoténuse =AB AC
et
cos(
̂
C)= adjacent de
̂
C
hypoténuse =CB CA
sin(
̂
A)=opposé de
̂
A
hypoténuse =CB CA
et
sin(
̂
C)= opposé de
̂
C
hypoténuse =AB AC
tan (
̂
A)= opposé de
̂
A
adjacent de
̂
A=CB
AB
et
tan (
̂
C)= opposé de
̂
C
adjacent de
̂
C=AB
CB

II – Outil indispensable : la calculatrice
Le rôle de la calculatrice va être de :
–donner la valeur du cosinus, du sinus ou de la tangente d'un angle ;
–retrouver l'angle quand on connaît le cosinus, le sinus ou la tangente.
Il faut vérifier que la calculatrice travaille bien avec des angles en degrés.
Si le cosinus de 90° ne donne pas 0, alors la calculatrice est mal réglée.
Selon les calculatrices :
–la touche 2nd s'appelle parfois shift.
–le cos-1 se note parfois arccos ou Acs
–le sin-1 se note parfois arcsin ou Asn
–la tan-1 se note parfois arctan ou Atn

III – Écrire une formule de trigonométrie
Exemple :
PRT est un triangle rectangle en R.
Donner la formule reliant les éléments en bleu.
Étape 1 : vérifier que le triangle est bien rectangle. Ok
Étape 2 : repérer l'angle aigu avec lequel on travail. C'est
̂
TPR
Étape 3 : repérer l'hypoténuse. C'est [TP]
Étape 4 : nommer les deux autres côtés :
Étape 5 : retrouver la formule utilisant les côtés qui nous intéressent : tangente
Étape 6 : écrire la formule.
tan(
̂
P)=opposé
adjacent =TR RP

IV – Trigonométrie : calculer une longueur ou un angle
Une fois la formule écrite, il faut isoler l'élément qui nous intéresse :
Exemple 1 :
on donne TR = 8 cm et
̂
TPR=35°
on peut calculer RP :
RP=TR
tan(
̂
P)=8
tan(35)≈11,4 cm (calculatrice)
Exemple 2 :
on donne TR = 8 cm et RP = 11 cm.
On peut calculer l'angle
̂
TPR
̂
P=arctan
(
TR
RP
)
=arctan
(
8
11
)
≈36 ° (calculatrice)