Fiche 1 - Trigonométrie - maths

Trigonométrie dans un triangle rectangle
Activité 1 : Rappel sur le vocabulaire
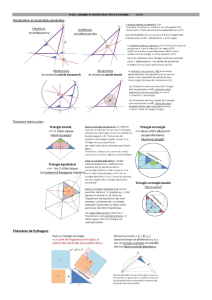
Le triangle ABC est rectangle en A.
[BC] est l’hypoténuse.
[AC] est le côté adjacent à l’angle C.
[AB] est le côté opposé à l’angle C.
Dans chacun des cas compléter les phrases :
Le triangle TQA est
……………………………………………………………… .
[………] est l’hypoténuse.
[………] est le côté adjacent à l’angle A.
[………] est le côté opposé à l’angle A.
Le triangle MPL est
……………………………………………………………… .
[………] est l’hypoténuse.
[………] est le côté adjacent à l’angle M.
[………] est le côté opposé à l’angle M.
Activité 2 : Rappel sur le cosinus
Les angles
I
$
et
µ
V
valent tous les deux 40°. Complète le tableau suivant :

2!
Trigonométrie,
Triangle
rectangle
Angle
considéré
Longueur du côté
adjacent à cet angle
Longueur de
l’hypoténuse
€
longueur du côté adjacent à l'angle
longueur de l'hypoténuse
IJK
I
$
=40°
€
..........
.......... =..........
WVU
µ
V
=40°
€
..........
.......... =..........
Que remarques-tu ?
……………………………………………………………………………………………………………………………
Quels sont les points communs entre ses deux triangles ?
………………………………………………………………………………………………………………………………
Prend ta calculatrice, et tape cos(40). Que remarques-tu ?
………………………………………………………………………………………………………………………………
…………………………….
Quelle formule pourrais-tu en déduire pour calculer le cosinus d’un angle ?
………………………………………………………………………………………………………………………………
…………………………….
Activité 3 : Utilisation de la calculatrice
Rappel :
Lorsque l’on connaît le cosinus d’un angle, pour déterminer la mesure de l’angle on utilise la calculatrice et on
tape :
Soit 2nd cos soit inv cos soit cos-1 soit Acos selon les calculatrices.
Complète le tableau suivant à l'aide de la calculatrice. Tu donneras la valeur arrondie du cosinus de
l'angle à 0,01 près et la valeur arrondie de l'angle au degré près.
------------------------------------------------------------------------------------
!"#$%&%$'!(! )!*+!,-.$/!&/,0!12!3,/.&/!4
!56! 7-+8/#$.,/!2&/#!9,2#/+:-#;/
!26 !"#$% & '(% & )%*+,)"-+.% & /0123 & 4'+5 &$-(5."'+5 &6#&
4%"4%()+$'6#+"%&7&/0123&4#55#(.&4#"&128&96#$%&'(&4-+(.&1&
5'" & $%..% & 4%"4%()+$'6#+"%8 & !"#$% &6# & )%*+,)"-+.% & /0138&
:;-+5+5&'(&4-+(.&<&5'"&/013&4'+5&(-**%&<2&62+(.%"5%$.+-(&
)%&/0123&%.&)%&6#&4%"4%()+$'6#+"%&7&/0123&4#55#(.&4#"&<8
!<6 ='% &)+"% & )%5 & ."+#(>6%5 & 0112 &%. & 0<<2&? & ='% & )+"% & )%5&
#(>6%5
!
1012
%.
!
<0<2
&?&@'5.+A+%8&1AA+$;%&6#&*%5'"%&)%&
$%.&#(>6%&)#(5&!"#$%(9-$;%8
!#6 B&62#+)%&)%&6#&A%(C."% &!"#$%&'D&#AA+$;%&6%5&E#6%'"5&)%5&
"#44-".5&
012
01
&%.&
0<2
0<
8
!=6 FG46#$%&6%&4-+(.&18&='%&"%*#"H'%5,.'&?&FG46#$%&6%&4-+(.&<8&='%&"%*#"H'%5,.'&?
!>6! ?'@-+0$,2$%-+
!26 B&62#+)%&)%5&+(A-"*#.+-(5&4-".G%5&5'"&6#&A+>'"%D&)G*-(."%&H'%&I1123&JJ&I<<238&
!<6 FG*-(."%&#6-"5&H'%&
012
0<2
K
01
0<
&%.&$-*46L.%&62G>#6+.G&012&M&0<&K&888&
!#6 FG*-(."%&H'%&
012
01
K
0<2
0<
8&='2%(&$-($6'5,.'&?
!=6 :%&"#44-".&%5.&#44%6G&6%&$-5+('5&)%&62#(>6%
!
1012
8&F#(5&6%&."+#(>6%&"%$.#(>6%&0112D&
%N4"+*%&6%&$-5+('5&)%&62#(>6%
!
1012
%(&A-($.+-(&)%&5-(&;O4-.G('5%&%.&)'&$P.G&#)Q#$%(.&
7&$%.&#(>6%8
!"#$%&%$'!A! )!7-0%+.0!/$!#21#.12$,%#/
!56! B!32,$%,!=/0!@/0.,/0
!26 ='%66%&%5.&62;O4-.G('5%&)'&."+#(>6%&"%$.#(>6%&
RS9&?&='%6&%5.&6%&$P.G&#)Q#$%(.&7&62#(>6%
!
9RS
?
!<6 TN4"+*% & 6% &$-5+('5 & )% & 62#(>6% &
!
9RS
& %(&
A-($.+-(&)%5&6-(>'%'"5&R9&%.&RS&4'+5&$#6$'6%,
6%8
!#6 T(&'.+6+5#(.&6#&$#6$'6#."+$%D&$#6$'6%&$-5
!
9RS
&%(&
"%*46#U#(. &
!
9RS
& 4#" & 5# & *%5'"%8 & ='%&
$-(5.#.%5,.'&?
!>6! B!1C2%=/!=/!12!#21#.12$,%#/
:-*46L.%&6%&.#V6%#'&5'+E#(.&7&62#+)%&)%&6#&$#6$'6#."+$%8&!'&)-((%"#5&6#&E#6%'"&#""-()+%&)'&
$-5+('5&)%&62#(>6%&7&WDWX&4"L5&%.&6#&E#6%'"&#""-()+%&)%&62#(>6%&#'&)%>"G&4"L58
!YZ[ X[ \W[ ]Z[
$-5&!WD^_ WD`` WD]Z
!"#$%&'()*+),)!-.%/0.
9
R
S
a&$*
\&$*
\W[