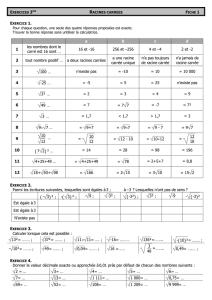
Racines de l`unité

I. El Hage www.les-mathematiques.net 1
Racines de l’unité
1 Racines de l’unité
Soit Kun corps et nun entier naturel non nul.
Définition Un élément a K est une racine n`
eme de l’unité si, et seulement si,
an1 .Soit SnKl’ensemble de toutes les racines n`eme de l’unité dans K. Cet en-
semble est non vide car 1 SnK.
Il résulte de cette définition que a K est une racine n`eme de l’unité si, et seulement
si, aest une racine du polynôme U X Xn1K X .
Exemple 1Kest une racine n`eme de l’unité pour tout n.iest une racine
4`eme de l’unité dans . j1
2i3 2est une racine cubique de l’unité dans .
Théorème Si mdivise n, alors SmK SnK.
Démonstration Si mdivise n, alors ns’écrit n pm où p. Il en résulte
a SmK am1anamp amp1a SnK
Théorème L’ensemble des racines n`
eme de l’unité SnKest un groupe multipli-
catif.
Démonstration SnK/
0comme nous l’avons vu. D’un autre côté, si aet bsont
des racines n`eme de l’unité, alors aet bsont non nuls et vérifient
ab 1nanb1nanbn11
ce qui prouve le théorème.
Définition On appelle corps premier d’un corps Kle plus petit sous-corps de K.
Théorème Le corps premier de Kest le sous-corps de Kengendré par 1.
Démonstration En effet, 1 appartient à tous les sous-corps de K. Il en résulte que
le sous-corps de Kengendré par 1 est le plus petit sous-corps de Kc.d. son corps pre-
mier.
Théorème Le corps premier de Kest l’intersection de tous les sous-corps de K.

I. El Hage www.les-mathematiques.net 2
Démonstration Facile à vérifier.
Théorème Le corps premier d’un corps Kest isomorphe à si sa caractéristique
est nulle, et à p(où (p) est l’idéal engendré par p dans l’anneau ) si cette carac-
téristique est p0.
Démonstration Soit ul’application de dans Kdéfinie par
u n n 1. Il est facile de vérifier que uest un homomorphisme d’anneaux et que
Im uest le sous-anneau de Kengendré par 1. Ker u est un idéal de . Il est engen-
dré par un élément pde . pest la caractéristique de K. Si p0, alors est isomorphe
à Im uet le corps des fractions de (c.à.d. ) au corps des fractions de Im u. Mais
ce corps est le plus petit sous corps de Kcontenant 1. Il est le corps premier de K.
Donc, si Kest de caratéristique nulle, son corps premier est isomorphe à . Si p0,
alors Im uest isomorphe à Ker u p qui est un corps (pest premier). Ce
sous-corps de Kest le sous-corps engendré par 1. Donc, si Kest de caractéristique
p0, son corps premier est isomorphe à p.
Exemple est le corps premier de et de . pest égal à son corps premier.
Théorème Soit Ple corps premier du corps K. Nous avonsU X Xn1P X .
Soit Rle corps des racines de Usur P. Si la caractéristique pde Kest nulle ou si elle
ne divise pas n, alors Rcontient nracines n`eme de l’unité distinctes.
Démonstration Il suffit de prouver que les racines du polynôme Usont toutes
simples. Sinon, Uet son polynôme dérivé UnXn1ont une racine commune. Or
zéro est la seule racine de Ucar p0 ou nest non divisible par p. Comme 0 n’est pas
une racine de U, toutes les racines de Usont simples et Ren contient n.
Pour démontrer que SnKest un groupe cyclique, nous avons besoin d’un théo-
rème de la théorie de groupes.
Lemme Soient aet bdeux éléments d’un groupe abélien multiplicatif G. Si
p Ord a et q Ord b sont premiers entre eux, alors Ord ab pq.
Démonstration Tout d’abord, gr a désignant le sous groupe de Gengendré par a,
gr a gr b est réduit à ecar si xest un élément de cette intersection, alors l’ordre r
de xest un diviseur commun de pet q. Cet ordre est donc égal à 1 (pet qsont premiers
entre eux) et x e. D’un autre côté, ab pq apbqee e. Enfin, si dest l’ordre de
ab, alors ab dadbd. Il en résulte adb1dgr a gr b e et par suite
ade bd. On en déduit que dest donc un multiple commun de pet q, donc de leur
produit car ils sont premier entre eux. Ainsi pq est l’ordre de ab.
Lemme Soient a1andes élément d’un groupe abélien multiplicatif G. Si les
ordres des a1ansont premiers deux à deux, l’ordre de leur produit est égal au pro-
duit des ordres de ces éléments.

I. El Hage www.les-mathematiques.net 3
Démonstration Par récurrence.
Théorème Si la caractéristique pde Kest nulle ou si elle ne divise pas n, alors le
groupe des racines nimes de l’unité SnKest un groupe cyclique.
Démonstration Soit n pn1
1pnt
tla décomposition de ncomme produit de nombres
premiers. Pour tout i1 2 til existe au plus n
piéléments aqui vérifient an
pi1,
car le polynôme Xn
pi1 possède au plus n
piracines. Soit, pour i1 2 t,aiSnK
tel que an
pi
i1. Considérons min
pni
iet biami
i. Les éléments bisont d’ordre pni icar
bpni
i
i1 et bpni1
i
isont différents de 1. Le produit bb1btest un produit d’éléments
dont les ordres sont premiers entre eux, il en résulte que l’ordre de best le produits des
ordres des bi. Ainsi best d’ordre n. Il engendre SnK.
Corollaire Le groupe des racines nimes de l’unité SnKest isomorphe à noù
ndésigne l’idéal engendré par n dans .
Définition On dit qu’une racine n`eme de l’unité est une racine n`eme primitive de
l’unité si, et seulement si, cette racine engendre le groupe SnK.
Si z SnKest une racine n`eme primitive de l’unité, alors
SnK1z z2zn1
Le nombre de ces racines primitives est celui des générateurs du groupe cyclique
SnK. Nous savons, d’après la théorie des groupes, que ces générateurs sont les zqoù
q1 2 n1 et qest premier avec n. Leur nombre est noté ϕnϕest en fait la
fonction caractéristique d’Euler.
Exemple Les racine 12`eme primitives de l’unité dans sont ω ω5ω7et ω11 où
ωexp iπ
6.
2 Corps finis
Les exemples les plus simples de corps finis sont les corps poù pest un
nombre premier et où p p .
Théorème Soit Kun corps fini. La caractéristique de Kest non nulle.
Démonstration Car sinon, le corps premier de Kserait isomorphe à .

I. El Hage www.les-mathematiques.net 4
Théorème Soit Kun corps fini. Si Card K q, alors Kest le corps des racines
du polynôme XqXle corps premier Pde K.
Démonstration Soit aun élément de K. Si a0, alors aqa0. Si a0, alors a
appartient au groupe multiplicatif de Kqui est un groupe fini d’ordre q1. Il en résulte
aq11 et aqa0. Ce qui précède prouve que Kest un corps de décomposition
pour XqXsur P. Il est un corps des racines pour XqXsur Pcar tout corps de
décomposition pour pour ce polynôme sur Pdoit contenir tous les éléments de K.
Théorème Soit Kun corps fini. Si Card K q, alors qest une puissance de la
caratéristique pde K.
Démonstration Kest un P-espace vectoriel. Si K:P n, alors
q Card K Card P npn.
Corollaire Deux corps finis de même cardinal ont la même caractéristique.
Démonstration Soient Card K q q les cardinaux et p p les caractéristiques
des deux corps. Nous avons pnq q p m
ce qui implique p p car ces deux entiers sont des nombres premiers.
Théorème Deux corps finis de même cardinal sont isomorphes.
Démonstration Soit Ket Kde même cardinal q. Soient Ple corps premier de K
et Pcelui de K.Pet Psont isomorphes car ils sont isomorphes chacun à p. Soit
σun isomorphisme entre Ket K. Le corps Kest le corps des racines pour XqXsur
P. Il est isomorphe à K, corps des racines pour XqXσXqXsur P.
Théorème Pour tout nombre premier pet tout entier n1, il existe un corps fini,
unique à un isomorphisme près, de cardinal q pn.
Démonstration Il suffit de prendre le corps des racines pour XqXsur P p .
Théorème Le groupe multiplicatif Kd’un corps fini Kest cyclique.
Démonstration Nous avons KSnKoù n Card K 1.