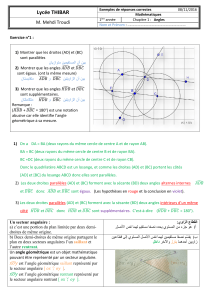
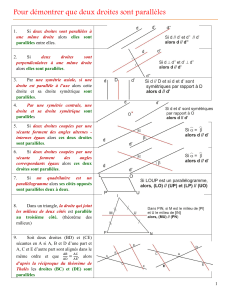
Modèle mathématique.

 Si deux droites et une sécante forment deux angles
correspondants égaux, alors les deux droites sont parallèles.
 Si deux droites et une sécante forment deux angles alternes
internes égaux, alors les deux droites sont parallèles.
d
d'
d
d'
35°
65°
80°
E
I
G
F
J
a
b
c
d
e
f
R
S
51°
b)
51°
a
b
c
d
e
f
R
S
35°
37°
a)
132°
48°
A
B
C
D
E
F
G
H
AB
C
D78°
100°
5ème
ANGLES ET DROITES PARALLELES
An4
 Dans chaque cas,
explique si les droites (uv) et
(xy) sont parallèles.
a) u t et z y sont des angles par rapport aux droites (uv) et (xy) et à la sécante (zt). AB alternes internes
Comme u t = z y, alors les droites (uv) et (xy) sont parallèles. AB
b) u t et x t sont des angles par rapport aux droites (uv) et (xy) et à la sécante (zt). AB correspondants
Comme u t n’a pas la même mesure que x t, alors les droites (uv) et (xy) ne sont pas parallèles. AB
 Recopie et complète :
Enoncé : Les points G,
B, E et F sont
alignés.
Les droites (AC)
et (DF) sont-elles
parallèles ?
Réponse :
 Les angles HEF et DEH sont … et
adjacents.
Donc DEH = 180° – … = 180° – …° = 132°.
 Les angles … et DEH sont … par rapport
aux droites (…) et (DF) et à la sécante (…).
 Comme ABE = …, alors les droites (…) et
(…) sont parallèles.
 Dans chaque cas, explique si les droites
(ab) et (cd) sont parallèles.
 Les droites
(xy) et (zt) sont-
elles parallèles ?
Justifie ta réponse.
 Les droites (IJ) et (GF) sont-
elles parallèles ? Pourquoi ?
conseil : calcule l’angle IGF ou IJE.
 ABCD est-il un
trapèze ? Justifie.
rappel : un trapèze doit avoir 2 côtés parallèles.
INFO
AB
u
v
x
y
z
t
36°
36°
a)
44°
46°
A
B
z
t
x
y
v
u
b)
x
yz
t
u
v
97°
63°
M
N