Effet Gyroscopique: Explication Simple et Compréhension Mécanique

L’effet gyroscopique
On sait que lorsqu’un mobile tourne sur lui-même à grande vitesse, son axe tend à conserver une
direction fixe dans l’espace, en l’absence de toute action extérieure. L’équation qui régit l’effet
gyroscopique est assez simple, mais n’est pas forcément « parlante » au commun des mortels.
Certes, si l’on nous dit : C=d(Iω/dt) (avec forme vectorielle pour C et ω) ce n’est pas très
compliqué, mais ça ne nous dit pas pourquoi les choses se passent ainsi. ( E=mC2 c’est simple
aussi….).
Je le dis d’autant plus simplement que j’ai longtemps ressenti un manque de compréhension du
phénomène. Savoir appliquer des formules, et devoir se contenter d’admettre ce qui se passe sans
justification est frustrant, en tous cas pour moi. Un jour je me suis mis en tête que « puisque le
déplacement d’un point découle toujours de F=M*γ, il doit être possible de raisonner à partir de là, et
généraliser ensuite à tout le mobile ».
Et ça marche : comme souvent, il est bon de revenir aux fondamentaux…..
La présente note explique en détail le phénomène gyroscopique, simplement à l’aide l’équation
générale de la mécanique F=Mγ. Cette approche très « terre à terre » permet une parfait compréhension
de la chose. Ainsi il devient facile de prédire le sens des mouvements, alors que beaucoup d’ingénieurs
auront besoin pour cela de la règle « des trois doigts », avec finalement un doute car on ne l’utilise pas
tous les jours, se demandant si c’est bien celle des trois doigts de la main droite, ou de la main gauche,
qui s’applique, et quel doigt représente quel vecteur…..
Ici, on « touche du doigt » le phénomène. En contre-partie, c’est un peu lourdeau, on ne peut pas
tout avoir…c’est pour ça que l’approche « officielle » garde tout son intérêt bien sûr. Mais c’est tellement
plus agréable une fois qu’on a bien saisi le truc….
La figure ci-dessous représente le mobile en rotation,
C’est un disque plan qui est représenté sur la figure, pour la commodité, mais peu importe : on
ne s’occupera que de la trajectoire d’un point M pris au hasard sur ce disque, de masse m, et
accessoirement du point M’ diamétralement opposé. Ayant pris le point M au hasard, la généralisation
sera ensuite légitime, pour tout le disque, ou pour tout objet de n’importe quelle forme (la symétrie n’est
même pas nécessaire, une patate va très bien du moment qu’elle tourne autour de son axe d’inertie).
Le mobile est supposé indéformable. Il tourne autour de son axe d’inertie, à une vitesse assez
importante, en tous cas par rapport à tout autre mouvement que l’on aura ensuite. Ces hypothèses sont
rappelées par souci de précision, mais on notera qu’elles correspondent à ce qui est attendu en général,
ni plus ni moins.
a) On examine ce qui se passe si l’on soumet l’axe du disque à un couple d’axe Oy (sur la figure,
il est appelé « couple de basculement appliqué »). Intuitivement, ce couple tendrait à faire
basculer le mobile dans le sens de la levée de M et de l’abaissement de M’, autour de l’axe
Oy.
Imaginons effectivement un début de rotation autour de Oy : la composante verticale
d’accélération en M et M’ est nécessairement proportionnelle à la distance entre M et l’axe y’Oy.
(sinon le disque se déforme, or par hypothèse il est rigide).
b) La distance de M à l’axe varie sinusoidalement dans le temps, conséquence de la rotation du
mobile autour de son axe, valant 0 en A et C, et son maximum (et son minimum) en B (et D),
cette accélération verticale de M et M’ varie donc sinsoïdalement aussi avec l’angle parcouru
par ces points.
il résulte de a) et b) que la composante verticale de la vitesse est maximale vers le bas en A et
maximale vers le haut C. Elle est nulle en B et en D.
c’est la fonction cosinus de l’angle parcouru, intégrale de la fonction sinus.

Ce résultat traduit exactement une rotation du disque autour de l’axe x’x.
CQFD !
« Le couple exercé engendre une mise en rotation (mouvement de précession) selon un axe
perpendiculaire à la fois au couple exercé et à l’axe de rotation principal.
« Le phénomène est parfait si le couple exercé est très petit par rapport au moment cinétique « du mobile
( = inertie du mobile * vitesse de rotation sur lui-même). Sinon le mouvement est perturbé sensiblement
(exemple de la toupie qui ne tourne plus assez vite).
Plus généralement, je propose une définition et quelques propriétés :
-le gyroscope est un solide en rotation rapide sur lui-même, soutenu par un système d’axes et de
cardans (ou équivalent) à très faible frottement. Sans perturbation extérieure, le mobile n’a
aucune raison de voir son orientation modifiée.
Remarque : même si le mobile ne tourne pas, il n’a aucune raison de voir son orientation
changer. Mais la rotation (associée à son inertie) lui confère une énorme capacité à conserver
sa direction propre. Et s’il y a une perturbation, la précession observée est un petit déplacement
en forme de cône, autour de la position de départ, qui n’est pas « oubliée ». Pour une simple
masse inerte, une perturbation (=une force, un couple) même non durable (comme un choc) va
lui donner une petite vitesse de dérive, qu’il va conserver pour s’éloigner de plus en plus de sa
position (force plutôt centrée) ou de son orientation (si c’est plutôt un couple, ou une force très
excentrée par rapport au centre de gravité).
-la Terre étant en rotation, l’axe du gyroscope restant fixe dans l’espace, on observe un
mouvement relatif fonction des directions relatives de la Terre et du gyro (comparable à
l’expérience du pendule de Foucault).
- si on applique un couple de basculement à l’axe du mobile, un basculement a lieu
transversalement au couple, avec une vitesse proportionnelle au couple appliqué, et qui subsiste
tant que ce couple est appliqué.
- si on oblige le mobile tournant à basculer, en forçant le mouvement, un couple résistant
apparait transversalement au mouvement de basculement imposé.
le couple exercé équivaut à exercer une force, donc une
accélération, vers le haut pour M, et vers le bas pour M’,
dont l’intensité est proportionnelle à la distance entre M
et l’axe y’Oy.
Les flèches représentent la composante verticale aussi
bien de la force exercée sur le point ( et son accélération.
M’
couple de basculement appliqué
y
y’
effet obtenu
M
x’
D
V
A
B
C
x
z
O
rotation du mobile
sur lui-même
(constante)
V’
effet attendu

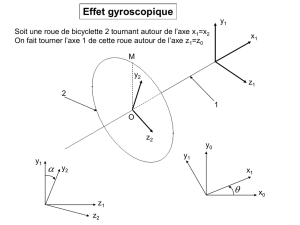
Discussion autour de l’expérience bien connue dite « de la roue de vélo »:
1) Prenez une roue avant de vélo par son axe, avec les deux mains tendues face à vous.
2) Quelqu’un la met en mouvement pour obtenir la vitesse la plus grande possible.
3) Essayer d’amener la roue dans le plan horizontal par pivotement des bras, l’un vers le haut l’autre
vers le bas.
4) Vous constatez que la roue « refuse » d’aller dans le sens voulu, mais qu’au contraire elle tend à
pivoter dans la direction transversale avant/arrière (ce qui n’est guère commode pour vous).
5) Si malgré tout vous insistez pour imprimer quand même le mouvement désiré, vous ne resentez
pas un couple dans le sens du mouvement que font vos mains tendues, mais transversalement,
c’est-à-dire que vous devez résister à ce mouvement transversale «que la roue voudrait avoir ».
Ce qui est difficile au départ, c’est de distinguer les mouvements et les couples que nous exerçons
de ceux qui sont une réaction du système et contre lesquels on ne fait que lutter.
En réalité, dans le mouvement que l’on fait, même en en forçant le sens, on ne produit aucun travail :
le couple auquel on résiste correspond au niveau de nos mains, à deux forces qui se déplacent
perpendiculairement à leur sens d’action.
Quand au couple que l’on doit exercer dans le sens de la rotation imposée, en fait il est nul, la rotation
se fait grâce au couple auquel on résiste, par effet « gyroscopique »….même si l’on a l’impression de
travailler… ! Cette impression est probablement aussi justifiée par la position assez incommade et
fatigante.
Raisonnons autrement : si l’on effectue un travail dans ce mouvement, où passe l’énergie
correspondante ??? nulle part puisque la vitesse du mobile sur son axe est constante (pas de frottement),
et la rotation cesse instantanément dès que l’on cesse d’imprimer le mouvement : il n’y a pas de notion
« d’élan » pris par le système, ou d’énergie cinétique supplémentaire qui serait emmagasinée quelque
part. Conclusion : aucun travail n’est fourni (ni reçu… !).
Encore une remarque.
Supposons que l’on effectue ainsi un demi-tour complet de l’axe. On retrouve donc la roue
tournant dans l’autre sens, à la même vitesse.
Une autre façon d’obtenir la même chose aurait consisté, sans modifier du tout son orientation, à
la ralentir, l’arrêter, la remettre en mouvement dans l’autre sens jusqu’à la même vitesse.
Dans un cas idéal on aurait pu charger une batterie en récupérant l’énergie du freinage, et
réutiliser cette énergie pour relancer la roue. On n’aurait donc, globalement, dépensé aucune énergie.
………..pour arriver au même résultat…….
Comme on sait bien que le bilan énergétique doit être le même globalement dans les deux cas, on
confirme qu’il n’y a aucun travail fourni.
Résumé de « la roue de vélo ».
-si on exerce un couple de basculement sur l’axe tenu à bout de bras, la roue aura tendance basculer
d’avant en arrière.
- si on résiste à ce basculement, on pourra obtenir le mouvement voulu, mais l’effort (ou le couple) à
fournir a changé d’orientation : on fournit un effort vers l’avant avec une main et vers l’arrière avec
l’autre.
On n’aura donc fait que décaler le phénomène : le couple sur un axe donne encore la rotation sur
l’autre….
Ce couple « auquel on résiste » engendre une vitesse de déplacement angulaire de l’axe, dans une
direction orthoganale. Si l’on arrête de « fournir » (ou : de résister à) ce couple, le mouvement s’arrête
instantanément. Ce mouvement est appelé mouvement de précession (de : précéder)…
Le mouvement forcé peut être présenté comme la succession de ces états :
- On veut une rotation de l’axe vers la droite (par exemple)

- On imprime donc un couple de basculement de l’axe dans ce sens (intuitivement).
- La réaction du système est en fait une volonté de basculement d’avant en arrière.
- Pour éviter ce basculement indésirable, on résiste dans le sens avant-arrière,
- Permettant ainsi au couple avant-arrière de naitre,
- Ce qui donne finalement la rotation voulue au départ.
On aurait pu, en connaissant le truc, pousser-tirer directement…..
Allons plus loin…..
On pourrait encore s’étonner de cette « similitude » (à l’inertie près) entre un couple, d’une part
et une vitesse de précession de l’autre (que l’on voit bien également dans la formule C=d(Iω/dt),
toujours avec notation vectorielle).
Une force ou un couple peut naître de façon quasi instantanée : « il y a cette force », ou « il n’y
a plus… », tandis qu’une vitesse ne peut être créée de façon instantanée : on crée l’accélération
(instantanée peut-être), puis la vitesse s’acquiert avec le temps. D’où une apparente petite incongruïté….
Il nous faut tout simplement admettre que le premier phénomène créé par le couple exercé est
conforme à la première intuition, c’est bien un « début d’accélération angulaire » tendant à basculer le
mobile dans le sens imprimé par le couple. Cette accélération proportionnelle au couple appliqué.
Toutefois, ce mouvement ne fait que naÎtre, et son effet est d‘autant plus minime que la valeur du produit
Iω est plus élévée. La plupart du temps on ne distingue pas ce début de mouvement, il est négligeable.
Par contre si la vitesse de rotation du mobile est insuffisante, il devient sensible.
Pour une toupie, par exemple, qui aurait trop perdu de sa vitesse, le fait de pousser latéralement
le dessus, par une espèce de pichenette, engendre une « sorte de précession », l’axe d’inertie du mobile
se trouvant écarté de la verticale et décrivant une forme de cône. La différence avec la précession
gyroscopique, c’est que quand le mouvement reste ensuite perturbé après que l’effet « parasite » (force,
couple) a disparu. C’est bien l’effet gyroscopique qui fait que la toupie ne tombe pas, mais la perturbation
a modifié son axe de rotation qui n’est plus confondu avec son axe d’inertie.
*****************
On sait que l’axe principal d’un gyroscope (parfait) ne dévie pas : il reste parallèle à lui-même.
On observe donc un déplacement angulaire de son axe, du fait de la rotation de la Terre, et d’autant plus
si on se déplace….
Un direction fixe dans l’espace, on imagine bien….
Mais que devient cette notion « d’orientation fixe » au cours des lustres, des siècles, des
millénaires…? quand on sait que le système solaire n’est qu’un tout petit morceau probablement pas fixe
de la galaxie, sans doute pas fixe non plus elle-même dans l’univers….
Les astronomes et astrologues….ont probablement la réponse…
Moi je voulais rester les pieds sur Terre…