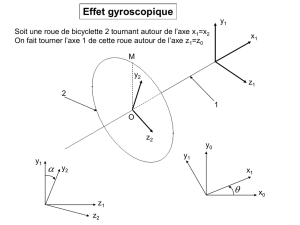
Berceau gyroscopique (cardans) avec roue de vélo (« toupie »)

Berceau gyroscopique
(« cardans »)
avec roue de vélo
(« toupie »)
Physique et ordres de grandeur

Roue de vélo gyroscopique
La roue de vélo ci-contre peut être lancée « à la
ficelle » au moyen de la poulie (noire) qui est
sur son moyeu. Elle est alors une « toupie »
gyroscopique qui « veut conserver la direction
de son axe de rotation » dans l’espace inertiel.
Ici, elle est suspendue dans un châssis qui la
laisse libre de ses mouvements autour d’un axe
vertical et autour d’un axe horizontal. Lancée
dans cette direction, son axe de rotation
horizontal fait « garde-cap » (en d’autres
termes, « gyroscope directionnel »).
Ce type d’utilisation (« suspendu à la Cardan »)
est étudié ci-après.
Mais…
Dans un autre atelier, on voit comment cette roue, tenue à bout de bras par un
opérateur, peut servir « d’appui gyroscopique » permettant de faire tourner
l’opérateur, même hors de contact avec le sol. Une utilisation qui a une parenté
avec ce qu’on appelle ailleurs un mode « gyrométrique ».

Schéma et notions de base
En bleu : « pivots » offrant toute liberté angulaire
Axe H
Moment cinétique
Axe T
Tangage
Axe C
Cap
Plancher
avion
La roue tourne autour de son axe H.
On utilise cette notation (H) pour
exprimer son moment cinétique
(voir plus loin).
L’axe de la roue est porté par le cadre
(« anneau de cardan ») jaune. Celui-ci peut
pivoter librement autour de son axe T (T
comme « tangage »… mais éventuellement R
comme « roulis », si l’avion change de cap…)..
L’axe T est supporté par une « fourche » (autre
« anneau de cardan ») verte. Celle-ci peut
pivoter librement sur une embase (bistre) qui
est solidaire du plancher du véhicule. C’est
l’axe C (C comme « cap »).
En plaçant un transmetteur d’angle sur l’axe C, on
distribuera un « cap directionnel » (pas
« magnétique » ni « géographique »).

H
C
L’essentiel en équations
F
F dH/dt
1- La roue a une masse M concentrée sur sa
circonférence de rayon R. Elle tourne à la
vitesse Ω (radians/seconde). Son moment
d’inertie : I = MR². Son moment cinétique H
= I Ω = MR² Ω. Sens du vecteur H : voir figure
(sens trigonométrique = anti-horaire).
2- L’opérateur (à l’arrière-plan) applique les
forces +/-F (couple C) sur l’axe de la roue
(main droite « à baisser »). Valeur de C = F
multiplié par distance entre F et –F. Sens du
vecteur C : voir figure (sens trigonométrique
= anti-horaire).
Ω
3- Equation de base du gyroscope (précession de la « roue-toupie ») : dH/dt = C (vecteurs H, C)
4- Commentaire : H reste constant en module, mais son extrémité s’éloigne de l ’observateur
de l’arrière plan. La vitesse angulaire (précession P) de H vaut : P = dH/H.dt = C/H. (rd/s)
5- Application numérique : M = 2 kg (masse roue) R = 0,3 m I = MR² = 0,2 m².kg environ
Ω = 10 rd/s (1,6 tour/s) H = I Ω = 2 m².kg/s Si C = 1 N.m (0,1 kgf.m) alors P = C/H = 0,5 rd/s

Une précession de précision
Axe C
Cap
Plancher
avion
1- Chaque cadre (jaune, vert) est doté d’un
« moteur-couple » (rouge) qui « essaie de le
faire pivoter ».
2- La flèche jaune représente un poids ou un
couple « essayant de faire tourner le cadre
jaune »….
3- Mais l’effet (gyroscopique) sera de faire
tourner la cadre vert ! « Précession » : un
gyroscope « fuit à angle droit ».
4- De même, un couple appliqué au cadre vert
provoquera une inclinaison du cadre jaune.
5- Moralité : si on veut maintenir horizontal
l’axe de rotation de la roue, c’est sur le moteur-
couple de l’axe C qu’il faut agir. Et…
6- Si on veut modifier (« réaligner ») la direction
de l’axe de roue (dans le plan horizontal), c’est
sur le moteur-couple du cadre jaune qu’il faut
agir.
7- Telles sont les « fantaisies » d’un « gyroscope
directionnel ».
Niveau
bulle