TD 2, 3 et 4 L`utilité ordinale, l`équilibre du consommateur et

TD 2, 3 et 4
L’utilité ordinale, l’équilibre du consommateur et la demande d’un
bien en fonction du prix et du revenu
Professeur Ahmed Ouazzani
Exercice 1. Karim, un étudiant habitant chez ses parents, dispose d’un premier temps de
120 DH d’argent de poche par semaine, il les dépense en achetant deux biens : la nourriture
et le loisir. Puis Karim a réussi à négocier une petite augmentation de son argent de poche
pour l’augmenter à 150 dhs.
A. Tracer la contrainte budgétaire de Karim pour chacun des situations suivantes (la
nourriture est portée en ordonnées et les loisirs en abscisses).
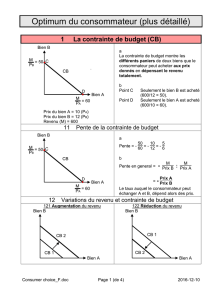
Budget
s
en dhs
points
P
n
prix de nourriture
P
l
prix du loisir
120
a
3
3
b
3
4
c
4
3
d
2
2
150
e
3
3
B. Commenter la ligne de budget des points (d) et (e) et comparer avec le point (a).
Exercice 2.Le tableau suivant présente une partie des préférences de Kamal pour la
nourriture (N) et le loisir (L) ; ces préférences prennent la forme de diverses combinaisons
des deux biens entre lesquelles il est indifférent. Chacun des trois jeux combinaisons a un
niveau d’utilité différent (les courbes d’indifférence correspondantes sont notées CI1, CI2,
CI3)
Les préférences de Kamal pour la nourriture (N) et le loisir (L)
Jeu d’utilité 1 (CI
1
)
Jeu d’utilité 2 (CI
2
)
Je
u d’utilité 3 (CI
3
)
L
N
L
N
L
N
2
40
10
40
12
45
4
34
12
35
14
39
8
26
14
30
16
34
12
21
17
25
18
30
17
16
20
20
21
25
22
12
25
16
27
20
30
8
30
13
37
15
40
5
38
10
44
13
50
4
50
8
50
12

A. A partir du tableau, tracer trois courbes d’indifférence ((la nourriture est portée en
ordonnées et les loisirs en abscisses).
B. Des trois courbes d’indifférences, laquelle présente le niveau le plus élevé d’utilité ?
C. Laquelle des trois courbes contient le plus faible niveau d’utilité ?
D. Soit les combinaisons suivantes de biens :
a ≈ (50(L), 8(N)),b ≈ (45(L), 4(N)),c ≈ (12(L), 45(N)), d≈ (25(L), 16(N)),
e ≈ (21(L),11(N))
Classer les cinq combinaisons par ordre décroissant de satisfaction.
E. L’information fournie dans cet exercice permet-elle de trouver le point de choix optimal
de Kamal ?
F. Tracer sur la graphique la ligne de budget du point (a) de l’exercice. Peut-on désormais
trouver la combinaison optimale de biens qui maximise l’utilité de Kamal ?
Exercice 3. Un consommateur maximisant son utilité choisit un point de tangence
entre sa droite de budget et une courbe d’indifférence parce que :
A. C’est la courbe d’indifférence la plus élevée qu’on puisse atteindre.
B. En tout point à gauche de la droite de budget, une partie du revenu ne se serait pas
utilisée.
C. Toutes les combinaisons de biens se situant à droite de la ligne du budget sont
inaccessibles compte tenu du revenu nominal.
D. Le point représente les prix relatifs les plus favorables.
E. En tout autre point de la droite budgétaire, l’utilité sera inférieure.
Laquelle des propositions suivantes n’est pas valable ?
Exercice 4. Représenter les cartes d’indifférence pour les deux biens X et Y dans les
situations suivantes :
A. Seul le bien Y fait l’objet de saturation ; le niveau de saturation est indépendant des
quantités possédées du bien X.
B. Seul le bien Y fait l’objet de saturation ; le niveau de saturation s’accroît lorsque le bien
Y est associé à des quantités croissantes de bien X.
C. C. le consommateur ne prend pas en compte le bien Y (on dit qu’il s’agit d’un bien
neutre).
D. Le consommateur n’aime pas le bien Y (on dit qu’il s’agit d’un bien indésirable)
E. Le bien X correspond à un repas dans un restaurant gastronomique, le bien Y
correspond à un disque de musique classique ; l’individu auquel on s’intéresse est
gourment.

Exercice 5. Karima possède la fonction d’utilité suivante :
U(x,y)=2xy+3y
Où x et y sont respectivement les quantités des biens X et Y.
A. A l’aide de deux méthodes, calculer le TMS ?
B. Calculer les coordonnées des points qui maximisent la satisfaction de Karima
C. Indiquer la valeur du multiplicateur de Lagrange, puis montrer que dU=λ .dR
D. Reprendre les questions c et d lorsque r=150, p=12 et q=21.
Exercice 6. On dispose d’une partie de carte d’indifférence de Samir relative à deux biens
X et Y, partiellement substituables et parfaitement divisibles. Les coordonnées de quelques-
uns des points de ces courbes d’indifférence sont présentées dans le tableau suivant, où U1,
U2, U3 correspondent à trois niveaux d’utilité totale et x et y représentent respectivement le
nombre d’unités des biens X et Y
U1
x
7
12
25
40
70
120
y
145
98
60
40
21
18
U2
x
18
20
30
50
70
120
y
140
115
85
60
44
38
U3
x
39
45
65
90
120
140
y
141
103
75
63
57
56
A. Représenter la carte d’indifférence.
B. Définir le TMS de X à Y et expliquer sa décroissance à mesure que x est substitué à Y le
long d’une courbe d’indifférence.
C. Samir dispose d’un Revenu nominal égale à 280 dhs qu’il affecte intégralement à l’achat
de X et de Y. Le prix unitaire de vente du bien X étant égal à 7 dhs et celui du bien Y est
égal à 2 dhs.
1. Définir la notion de droite du budget du consommateur, déterminer l’équation
de cette droite et utiliser le graphique précédent pour la représenter.
2. Déterminer graphiquement l’équilibre du consommateur (point E1, sur le
graphique) et donner la signification économique de ce résultat.
D. Si, « Certeris paribus », « toutes choses étant égales par ailleurs », le prix unitaire du
bien X baisse et devient égal à celui du bien Y :
1. Déterminer le nouvel équilibre du consommateur (point E2).
2. Analyser le passage du point d’équilibre E1 au point d’équilibre E2 en mettant
en évidence l’effet revenu et l’effet de substitution qui l’expliquent. Utiliser la
méthode de J.R Hicks et E.Slutsky.
3. A quelle catégorie de biens appartient le bien X ?
E. A partir des informations disponibles, construire la courbe de demande individuelle du
bien X en fonction de son prix.

Exercice 7. La figure suivante montre comment Karima réagit à la baisse du prix des
Shawarmas alors qu’elle a le choix entre les Shawarmas et les Brochettes.
AB est la ligne de budget d’origine et 0X1 la quantité de Shawarmas achetée par Karima, Après la
baisse du prix, la droite de budget devient AC et Karima consomme la quantité 0X2 de Shawarmas.
A. Illustrer les effets de revenu et de substitution contenus dans la réaction de Karima à la baisse de
prix.
B. Les Shawarmas sont-ils un bien normal ou un bien inférieur ?
C. Les effets de substitution et de revenu se renforcent –ils mutuellement ou agissent-ils dans les
sens opposés ?
D. Dans quelles circonstances l’opposé serait-il le cas ?